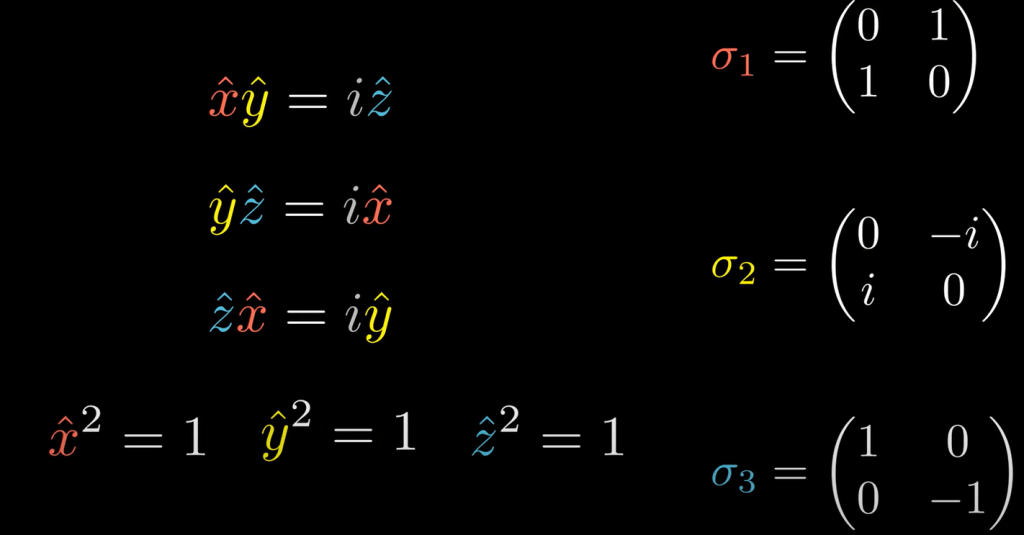Stumbled upon this swift introduction to Geometric Algebra and I feel so overjoyed. It is made by opensource math animation tool – https://github.com/ManimCommunity/manim, where 3B1B is the major contributor.

The way it is unfolded is natural and intuitive. As a start we all are familiar with real numbers which is just zero rank/dimensional scalar. And we learn 1-D vector, so there must be higher dimensional objects…

Based on our understanding of 1-D Vector, the 2-D object or Bivector can be conceived in similar way: the length is area, adding two bivectors is as below, and when introducing the basis bivector, we can easily conduct adding etc. operations algebra like trivial.

Now comes the ultimate definition of geometric product that is mind-blowing. It is made up of inner product and outer product, standing for a reduction to a scalar and upgrading to a bivector. It is the HEART of geometric algebra!

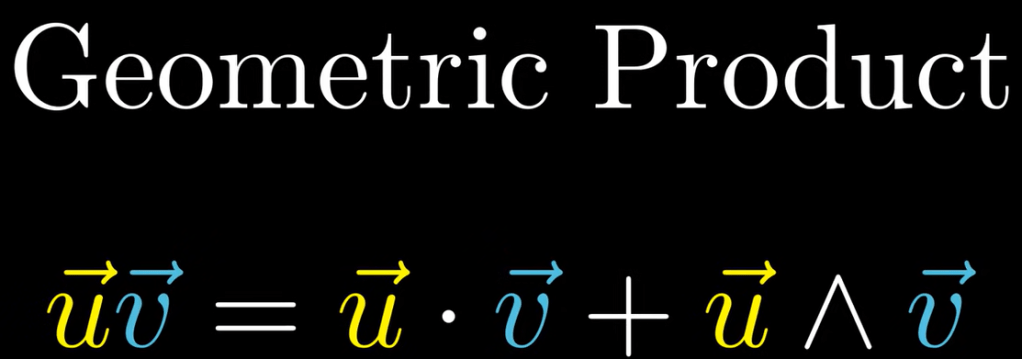
If we product a vector u itself, it just turns out to be the magnitude of u squared and the outer product term is vanished. By the same vein, we can derive other forms of operations between two 1-D vectors.

So the basis metric i, j, k can be expressed

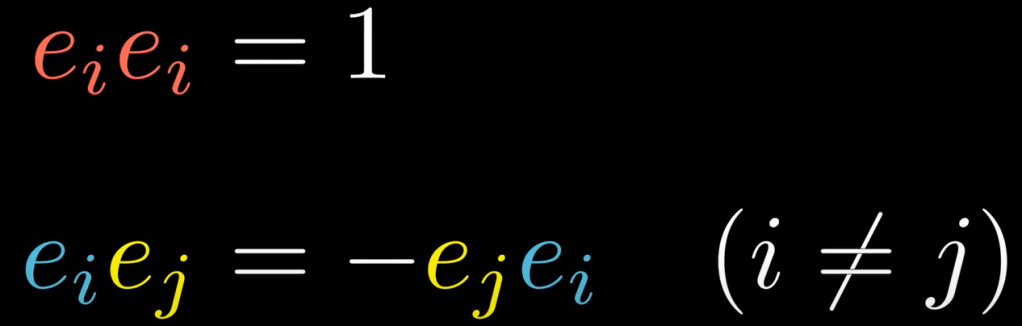
So we can perform product of two vectors u and v as

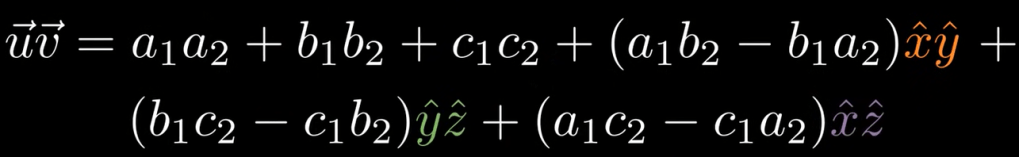
Here comes the bomb, in describing 2D, 3D vectors we simply call x hat y hat i, yes, i like in the imaginary part unit in complex numbers. This i plays a magical rule in multiplying operation, for example, use i to multiply any random vector

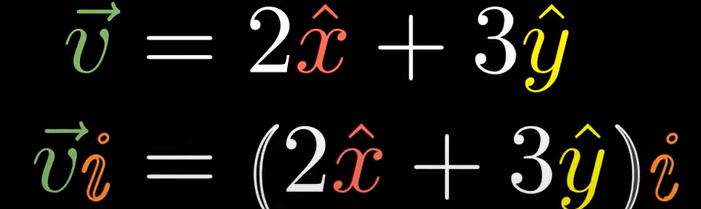
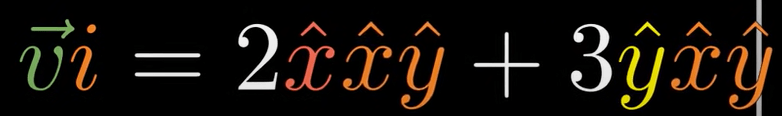
It turns out multiplying i is same as rotating vector to left side by 90 degrees. If put i in front of v, it is rotating v to the right side. And if we rotating i itself, processing the algebra, we get i squared is negative 1. Exact as in complex numbers. Hence, we say complex numbers are actually the sum of a scalar and bivector!

Everything in math connects now!

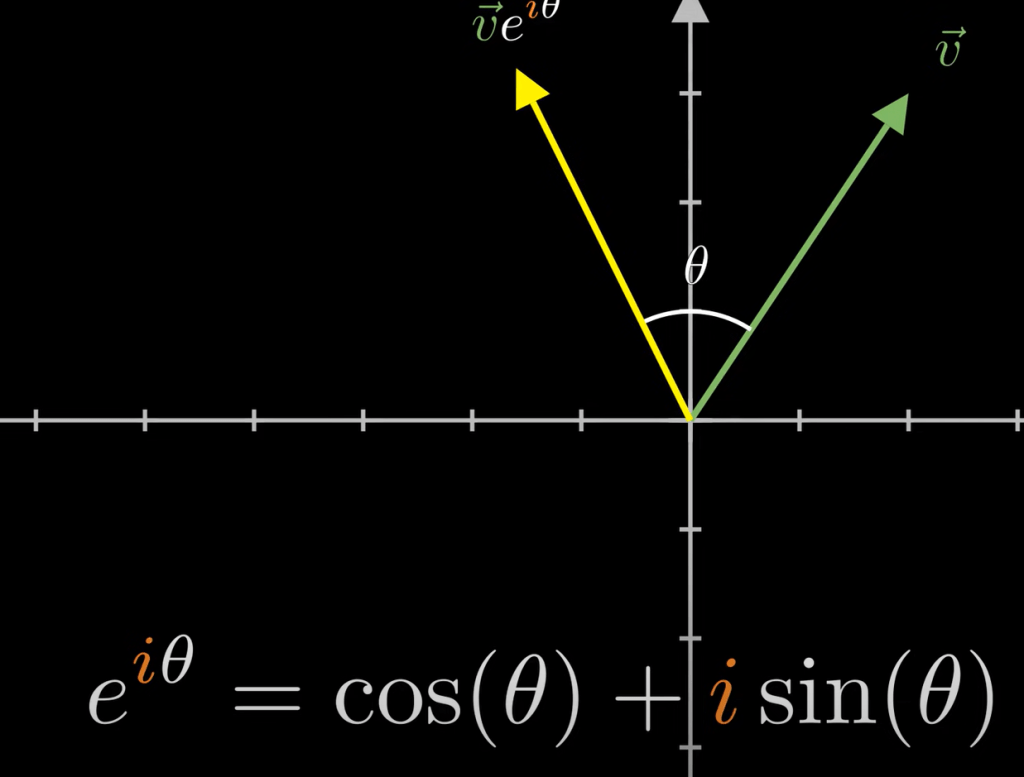
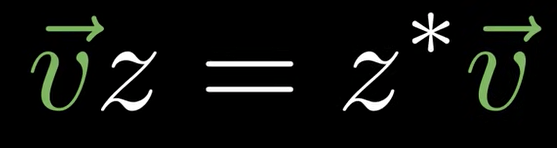
So multiplying a vector is also interpreted as rotate to theta decided by the angle between two and then scaled up by the magnitude of the vector.

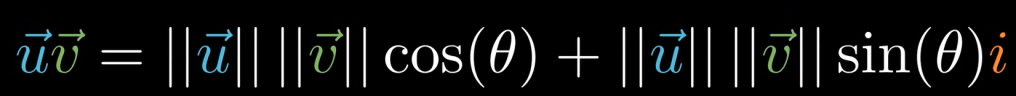
Moving on the 3D geometry:

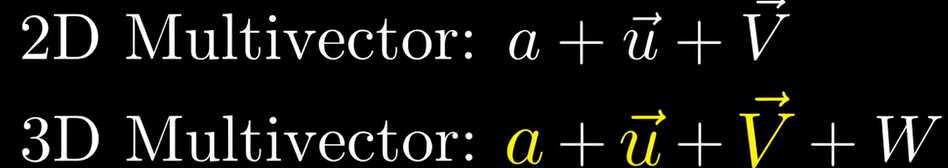
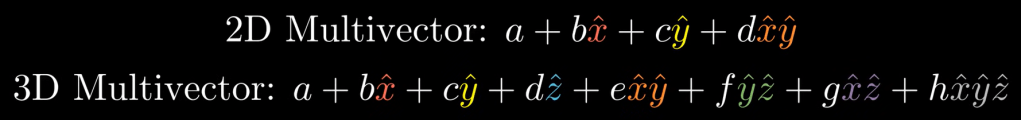
There are differences between 2D and 3D, first,

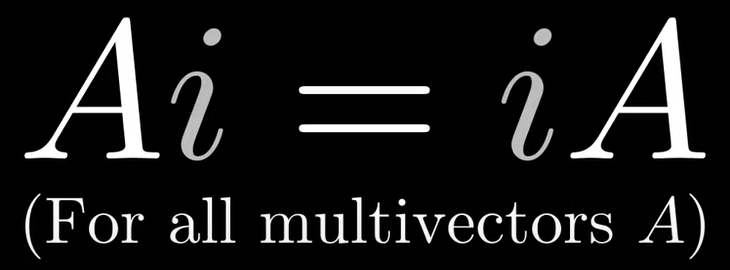
So geometrically we can see the conversion between two (reminiscent of cross product and right hand rule)

Actually we can get

So cross product is an unnecessary concept invented by mathematicians. We can pretty much live a simpler math life with only the outer product concept.

If we play around the basis vectors as below, we recognize it’s the Pauli square matrices.