This blog is aimed to solve the text book page 37 question 27 and 28:

“For each of the points aand planes listed, find the distance from the point to the plane or line. Is the point on the same side of the plane or line as the origin, or on the opposite side? Is the point above the plane or line, or below it(Where up is the direction of the positive y-axis in R2 and the direction of the positive z-axis in R3)?
27: point(1, 0, -1); plane x +2y + 3z = 1. 28. point(-2, 1, 0); plane x -y + z = 2″

How to even approach this question. let’s start from the basic description of equation of lines or planes by knowing the perpendicular vector p. like shown below: knowing a fixed point x0, perpendicular vector p, try to find/describe the set of points x,

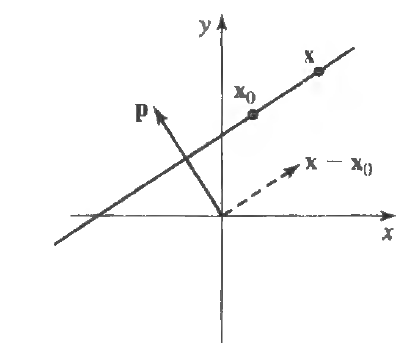
So according to the dot product output,

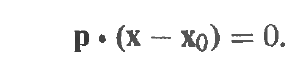
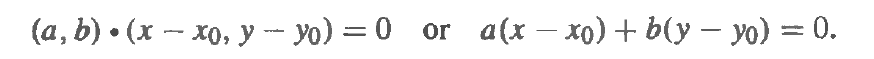
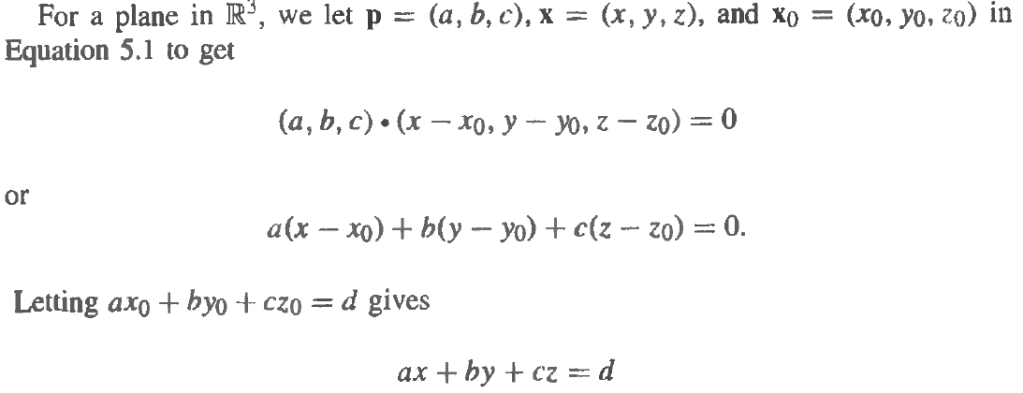
So, if given a vector p and a fixed point, we can deduce the plane passing through the point while perpendicular to p:

On the other hand, if given the plane and a vector p, and a random point x1 or x2, we can use a normalized equation to find the distance, measured perpendicularly, from a point to a line or plane, as is shown below the delta.

What is the normalized equation?

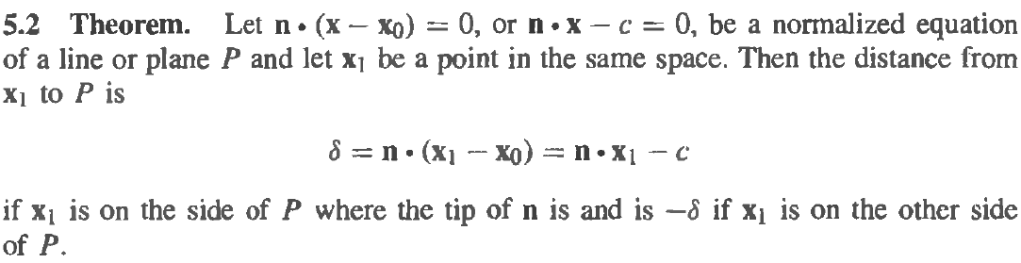
Here is an example of application:

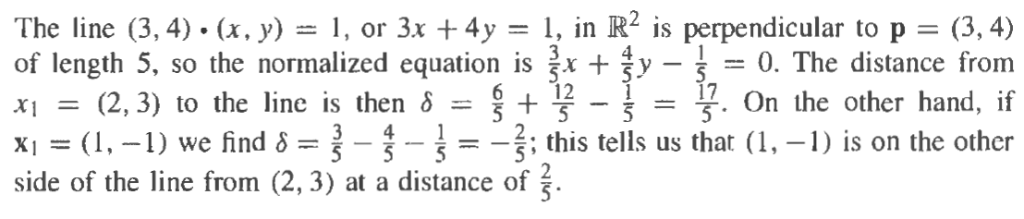
Note if it’s not normalized vector n, the above approach won’t hold. Why?

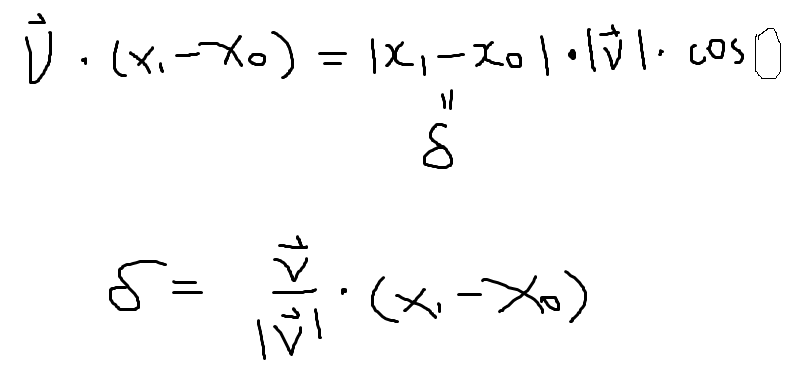
X0 is the dot on the plane so vector v dot X0 is always the right side of the plane equation.

Note the above equation has a huge mistake that I confused X0 to be the intersect dot between given point vector and the plane. it should be another intersect dot, we name is X3, shown below

Now to solve the homework problem 27:

normalize the equation:

plug in (1,0,-1), we get -3/sqrt(14).