There are three levels of progression in thematic indexing:

Level 1, rudimentary, via industry business classification such as GICS and RBICS;

Level 2, supply chain expansion via combination of industry classification system and supply chain data;

Level 3, timely and forward-looking via machine learning techniques such as LSI, LDA.

In this article, I aim to test and discuss LDA application in Thematic Indexing practice by the US companies with transcript documents as text corpora. I will first outline a review of LDA techniques and then dive into data collecting and processing, lastly I will analyze the outcome and discuss the outlook for applying this technique in thematic indexing.

Latent Dirichlet allocation (LDA) has been documented in a comprehensive paper authored by David M. Blei, Andrew Y. Ng, and Michael I. Jordan in their paper “Latent Dirichlet Allocation” published in Journal of Artificial Intelligence in 2002.

Right at the beginning, the authors states that the goal is to perform basic tasks “such as classification, novelty detection, summarization, and similarity and relevance judgments” via an efficient processing of large collections text corpora or other large amount of discrete data. It is been studied or covered in the subject called Information Retrieval(IR).

Earlier in 1983 ((Salton and McGill, 1983), tf-idf scheme was raised and applied. However, it has the shortcomings of “small amount of reduction in description length and reveals little in the way of inter- or intra document statistical structure”, LSI was proposed to address them by (Deerwester et al., 1990). “LSI uses a singular value decomposition of the X matrix to identify a linear subspace in the space of tf-idf features that captures most of the variance in the collection. This approach can achieve significant compression in large collections.” But there is the fitting problem related to this generative model. So Hofmann (1999) presented the probabilistic LSI (pLSI) model, also known as the aspect model, as an alternative to LSI. Hofmann’s work still provides no probabilistic model at the level of documents.

All above are based on “bag-of-words” assumption, neglecting the order of words could change the meaning. A classic representation theorem due to de Finetti (1990) establishes that any collection of exchangeable random variables has a representation as a mixture distribution—in general an infinite mixture. This line of thinking leads to LDA.

LDA as a dimensionality reduction technique, in the spirit of LSI, but with proper underlying generative probabilistic semantics that make sense for the type of data that it models. LDA can be readily embedded in a more complex model which is a property that is not possessed by LSI.

What these authors aim in the paper is to capture significant intra-document statistical structure via the mixing distribution. Moreover, it uses the simple “bag-of-words” models, which lead to mixture distributions for single words (unigrams), our methods are also applicable to richer models that involve mixtures for larger structural units such as n-grams or paragraphs.

What does Dirichlet in LDA mean? It refers to Dirichlet distribution (after Peter Gustav Lejeune Dirichlet), is a family of continuous multivariate probability distributions parameterized by a vector alpha of positive reals. Dirichlet distributions are commonly used as prior distributions in Bayesian statistics.

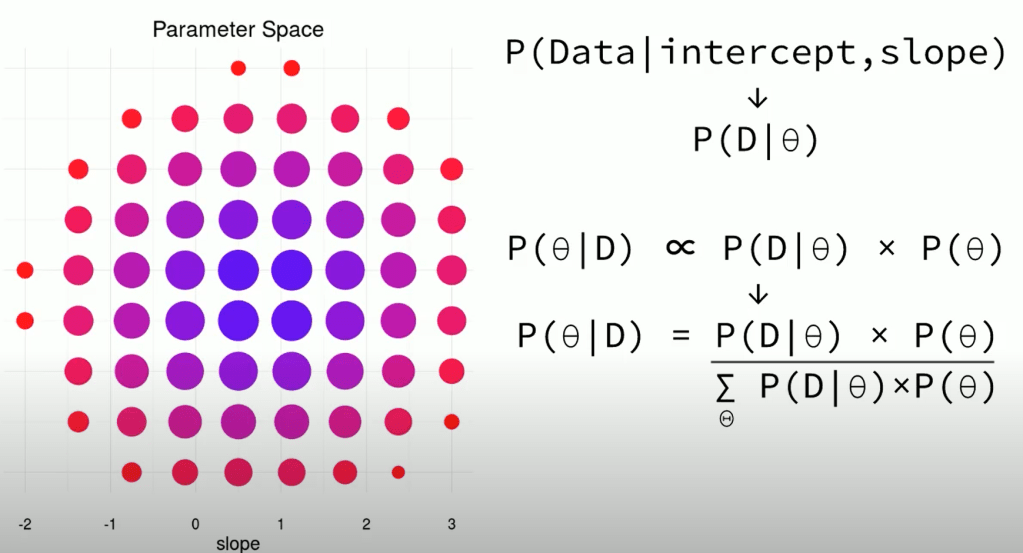
Since the generative model is essential, I will digress to go over Bayesian data analysis, particularly in what, why and how. via this clip. It is a method for figuring out unknowns that requires data, a generative model and priors, what information the model has before seeing the data.

My intuitive thought about this Bayesian data analysis is simple – knowing there is a fixed percentage of an event in a large population, we do massive amount of sample test, given the sample test rate frequency chart, we can infer the actual fixed percentage:

The mathematic expression is

This is consistent to the classical Bayes formula: P(B|A) = P(A|B) * P(B) / [P(A|B) * P(B) + P(A|~B) * P(~B) ], or better illustrated in below explanation slide the same instructor Baath provided:

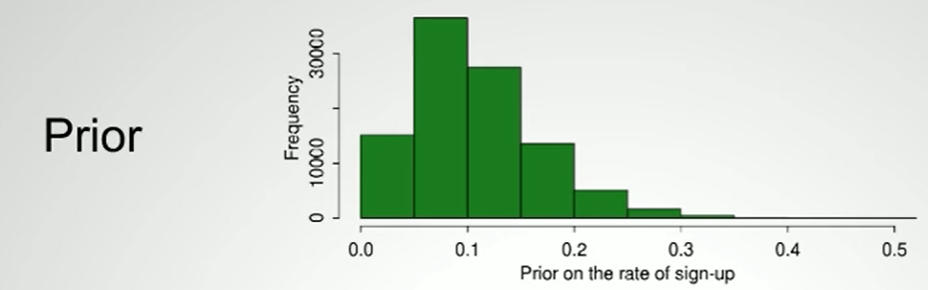
Note the prior can be changed such as below reflecting expert view

Markov Chain Monte Carlo is a class of algorithms that samples from probability distributions by walking around in the parameter space. the programming language is stan, and we use it together with Python