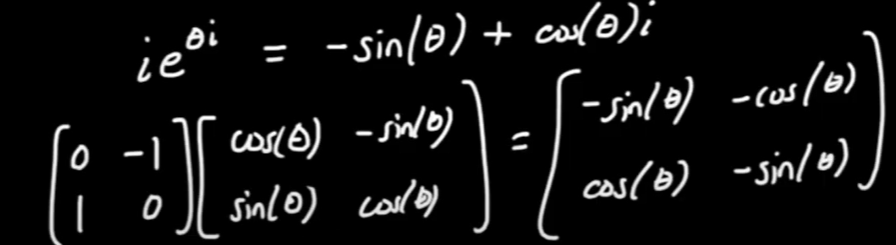Even it’s not the first time I got to learn all these majestic and unthinkable fact that the abstract concepts of complex number, exponentials are profoundly identical underneath, Mathoma’s interpretation is still quite mind-blowing.

Starting from basics

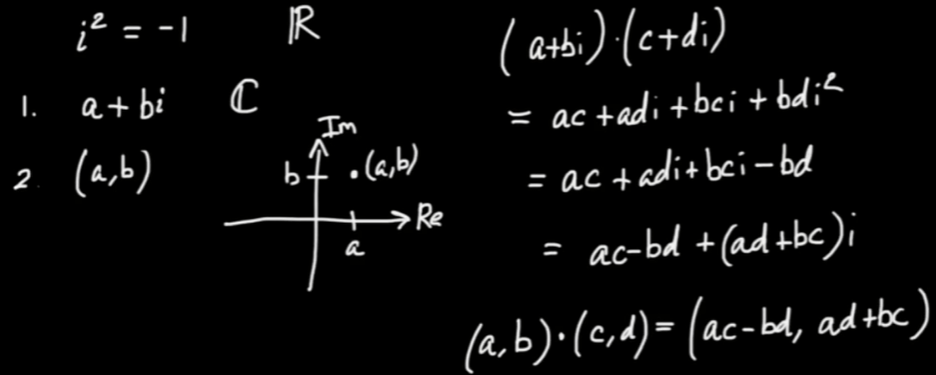
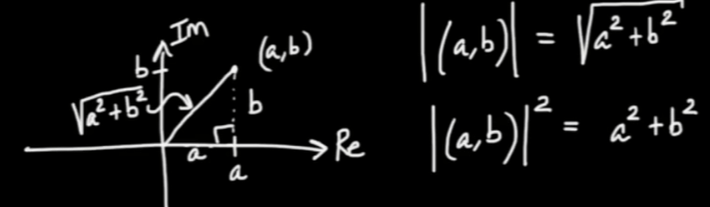
The magnitude/module/length is expressed as

If we pick |B| = 1, it is a circle, so the multiplication is just moving A around according to the theta of B moving; if |B| = 2, then not only it applies the same moving but also stretching by the unit of |B|=2.

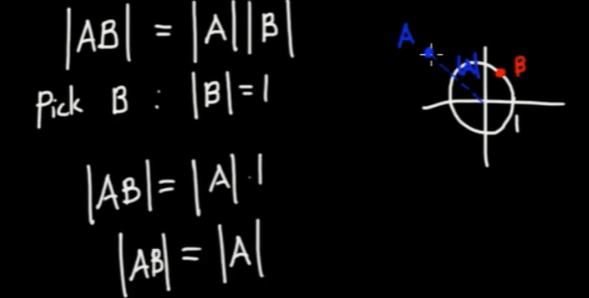
The circular equation is also expressed as trigomatory terms

Further, with tiny angle moving we also add bit of stretching by 1.025:

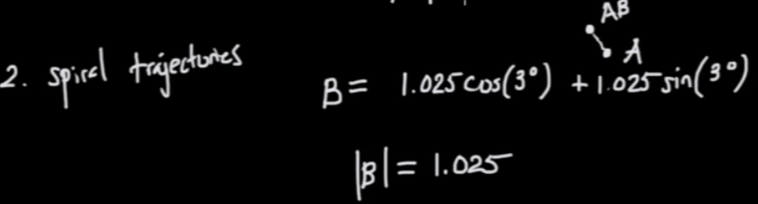
If we apply both stretching and rotating it can show as a spiral expanding universe.

Above, we get an intuitive feeling how multiplying another complex number using trig expression can realize rotating and stretching, next, we try to infer the equation of (a, b) rotating a slight position (angle theta) around the origin to (a, b)’:

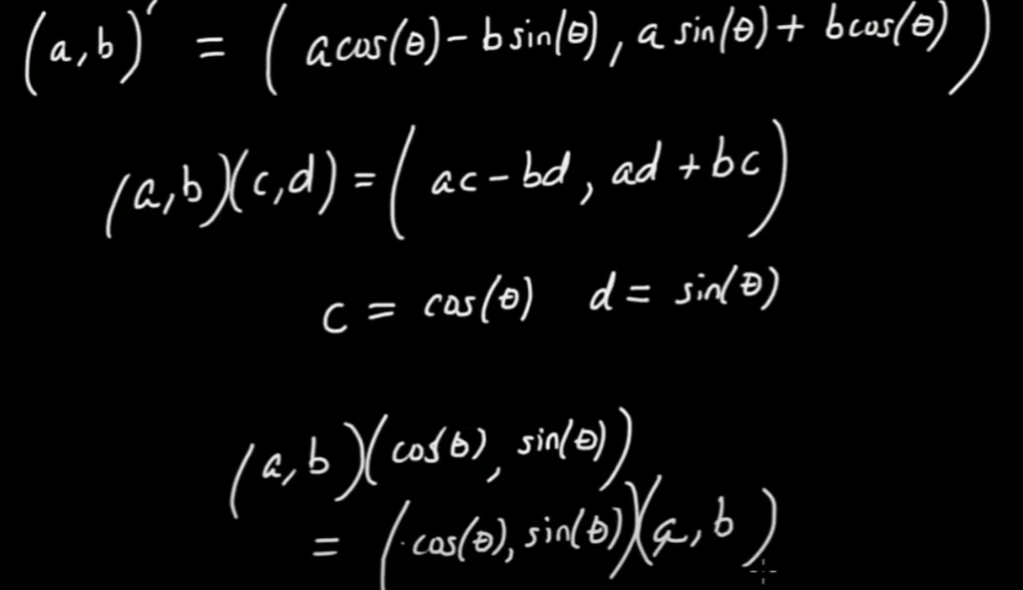
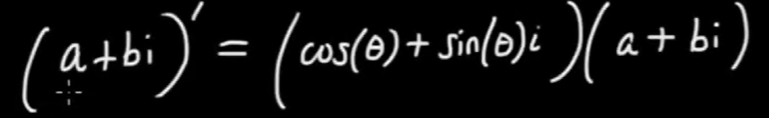
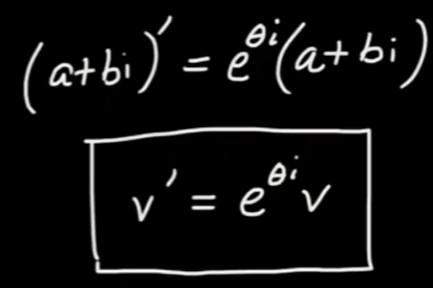
Rotating 90 degrees anti-clock wise is

Lastly, complex number also can be written in matrix form:

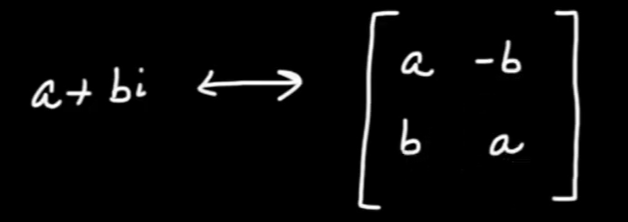
so if we multiple complex number (a+bi) to (c+di)

So the matrix operation is commutive and conjugate matrix is the transpose form.

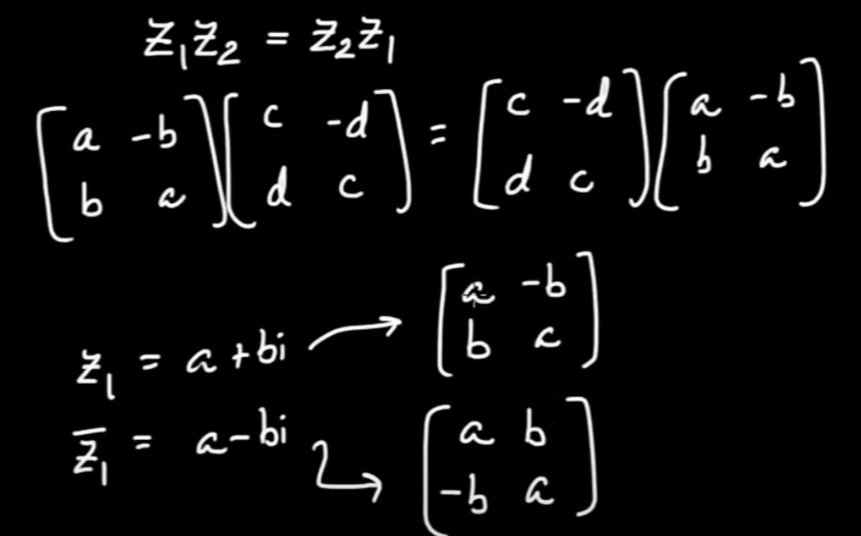
In matrix there is an important concept of determinant, it turns out to be the length of the matrix per below deduction.

Euler’s formula unified exponential to complex number and hence, matrix,

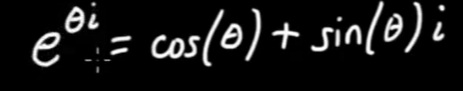
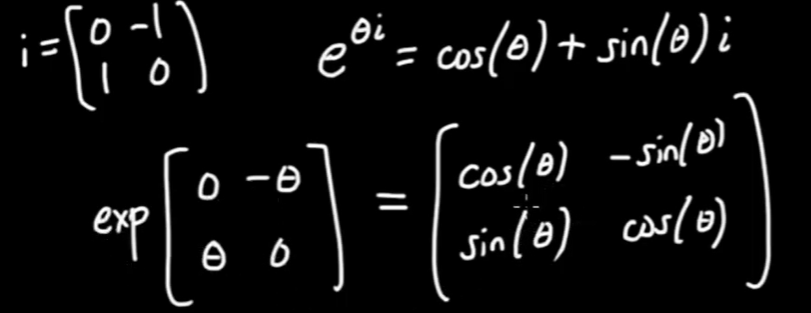
What’s more beautiful is that it makes it possible to conduct calculus in matrix, complex numbers because exponential form is the most uniquely simple way to be differentiated-itself.