The beauty of math is it taught me to view things in various ways. Even the foundation of mathematical description can be different. Brought up in rigid Descartes coordinate system, my mind is so liberated to learn complex number, dot product, inner product, vector space to now Geometric Algebra and Quaternion system.

It was invented by an Irish mathematician Hamilton in the 18th century, follows exact same logic as we learn matrix, but instead of in 2 or 3 dimension, it sets 4D. Any quaternion can be expressed as q = (a, b, c, d) or = (scalar a, vector formed by (bi, cj, dk)).

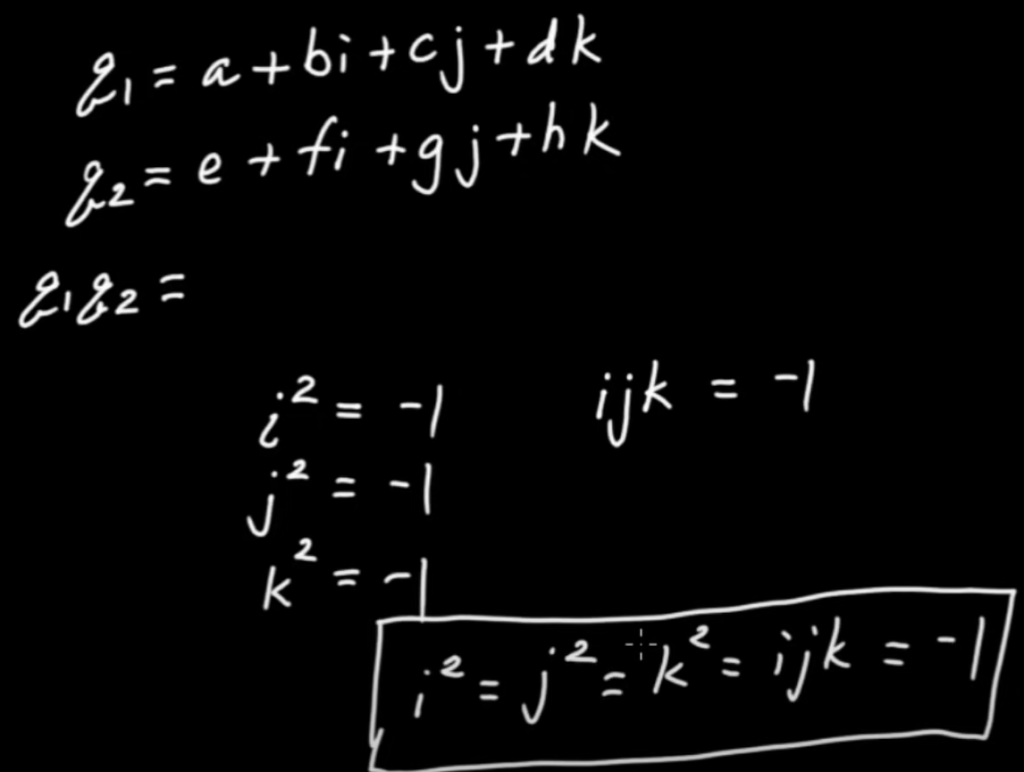
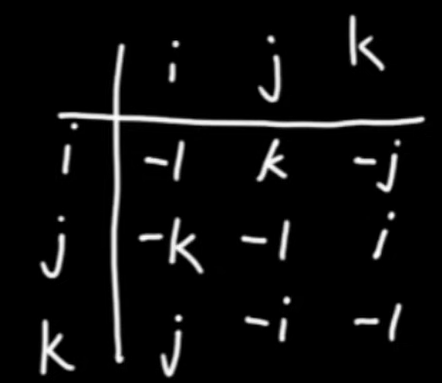
Then we can deduce the multiplication of quaternions. From observation below, mathematicians naturally tends to put this quaternion into matrix (4×4) form as laid out below:

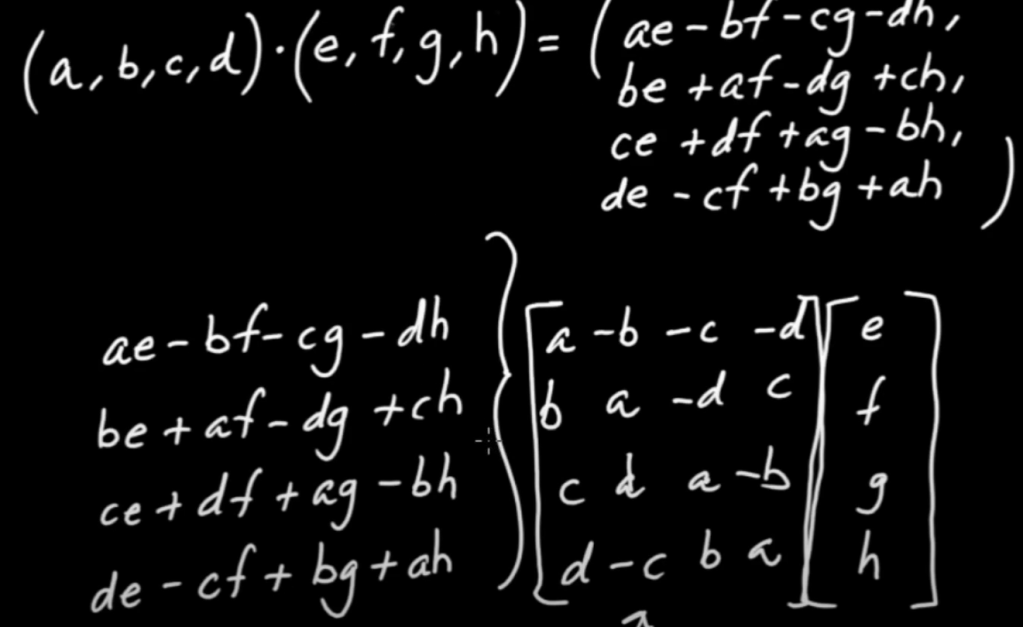
so the unit quaternion is

Dot product of two quaternions:

And the below part really is a genius’s work to make that insightful observation and summarize to

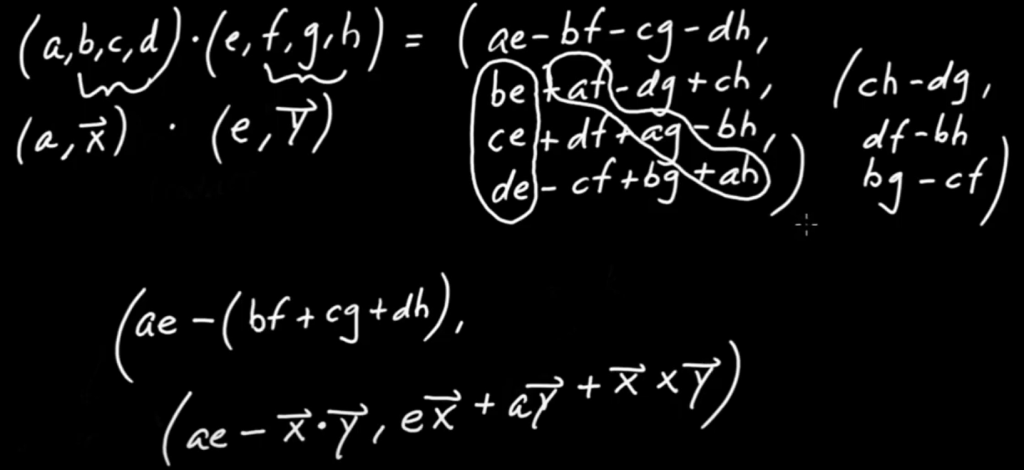
Rewritten as

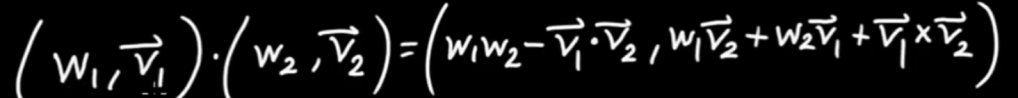
If we rid of the scalar part, then

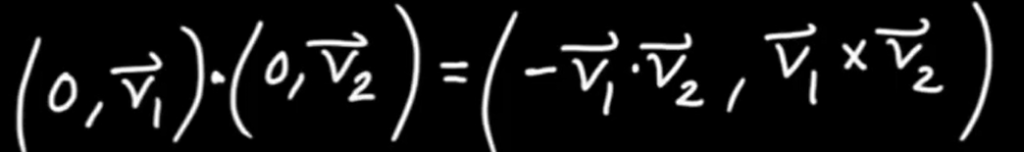
Some further manipulation can be done to draw connections

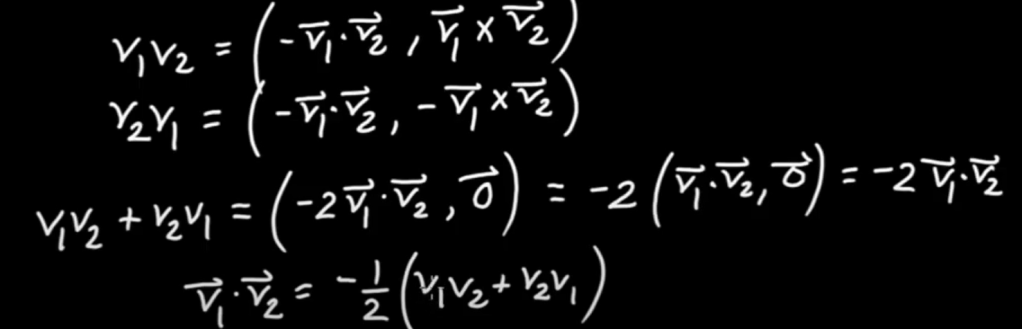
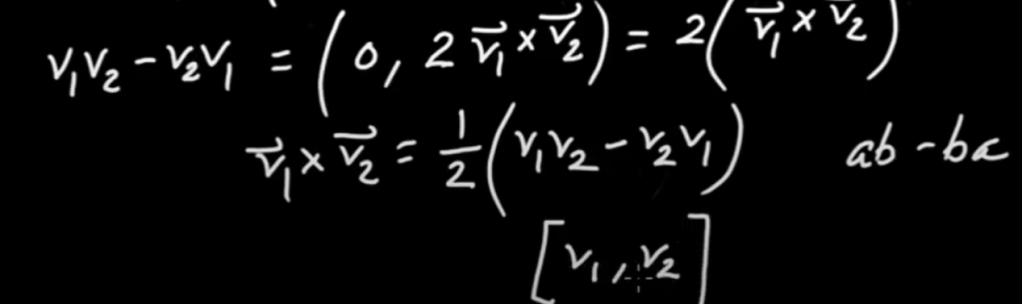
Quaternion is very important in solving problems such as 3D rotations.