Operator especially Hamilton Operator is essential in QM. So it’s worthwhile to dig deeper of this concept.

From this professor Gabriele Carcassi, I learned a brand new perspective in understanding Operator. It’s all related to the familiar “vector field” composed of position x and momentum p.

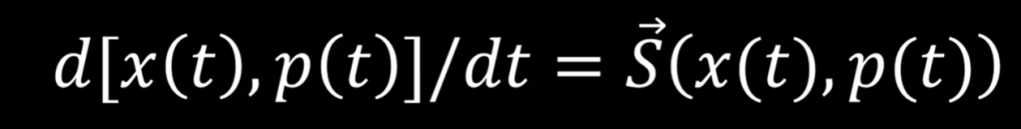
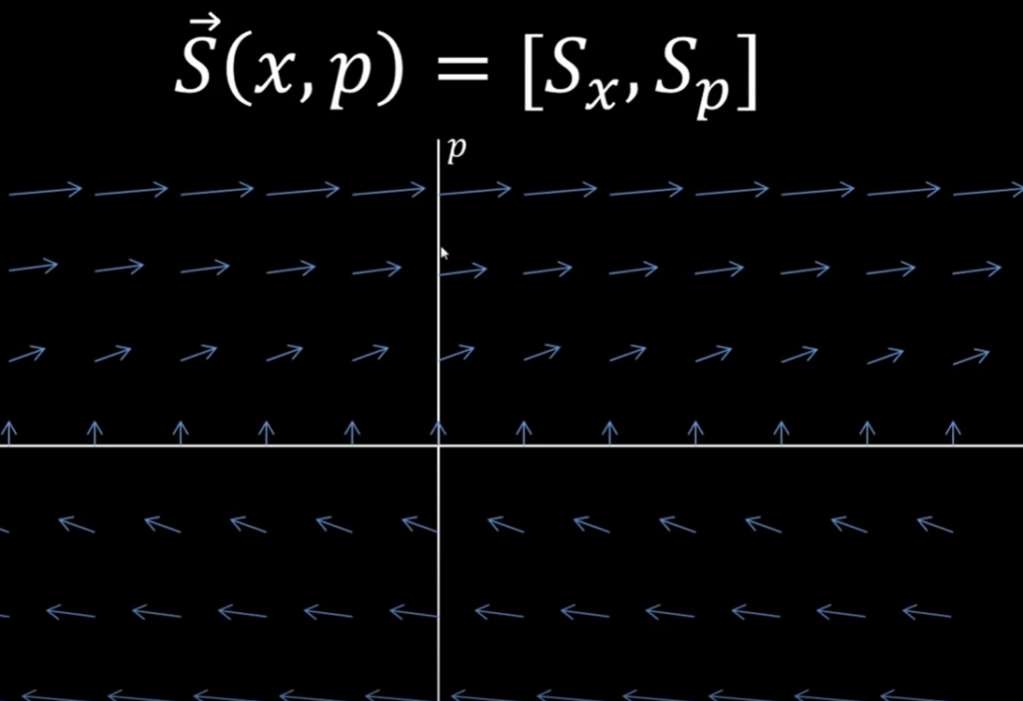
Now look at H defined/composed by/of x and p, which both are parametrized by t, is a scalar.

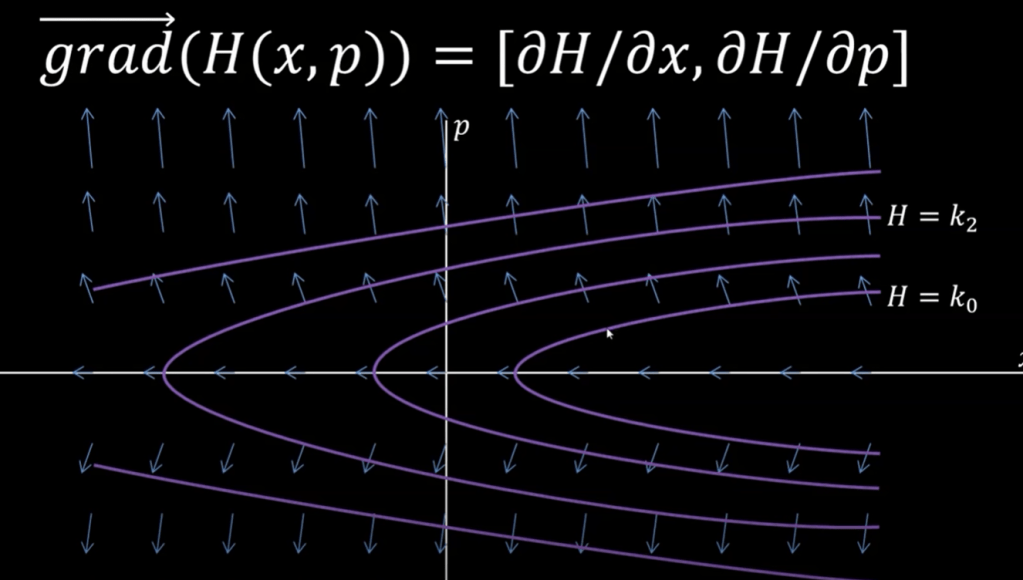
If we rotate 90 degree of the gradient, it’s exactly the former vector field S:

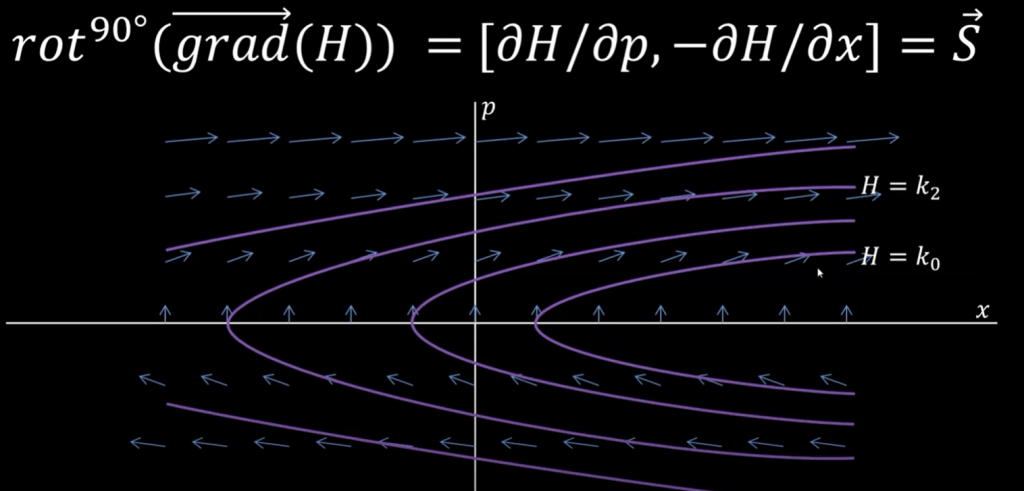
Above view is novice but still hard to fully take, switching gear to classical understanding by Faculty of Khan, in the sense of finite dimensional space Operator can be thought of as an matrix.

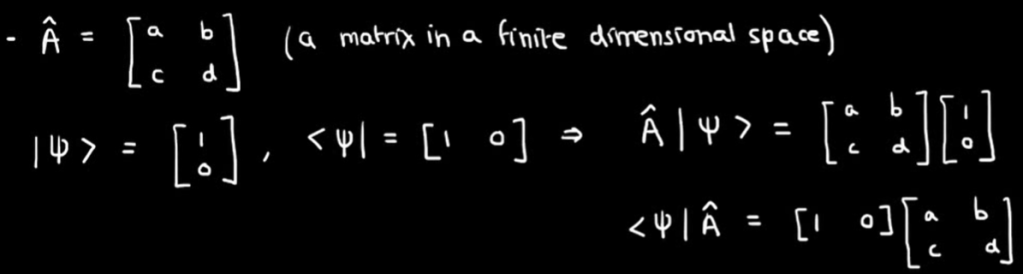
But in function space, operators aren’t generally written as matrices, it’s an operator acting on the other side:

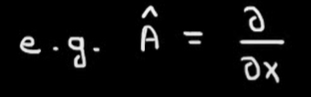
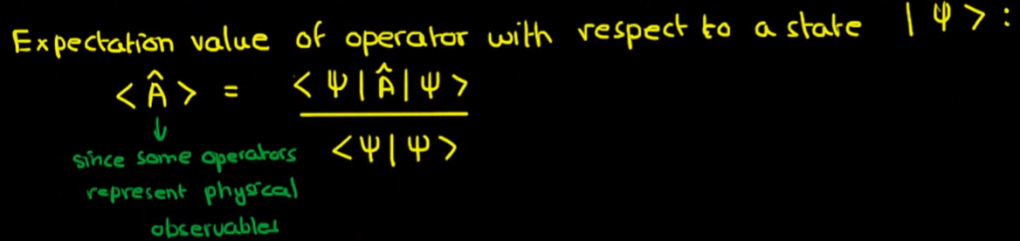
There are Inverse Operators, Hamilton Operator, Unitary Operator and Projection Operator.

Why Hermitian Operator is emphasize in QM? My understanding is that the rule/definition Hermitian Operator leads to the computation of eigenvalues to be real, this means that it makes sense to have Hermitian operators as observables. it’s said the expectation value of operator with respect to a state sai is an observable. In physics, Observables are magnitudes we can measure: position, momentum, angular momentum, charge, etc.

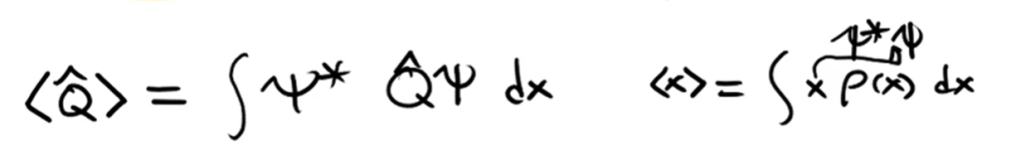
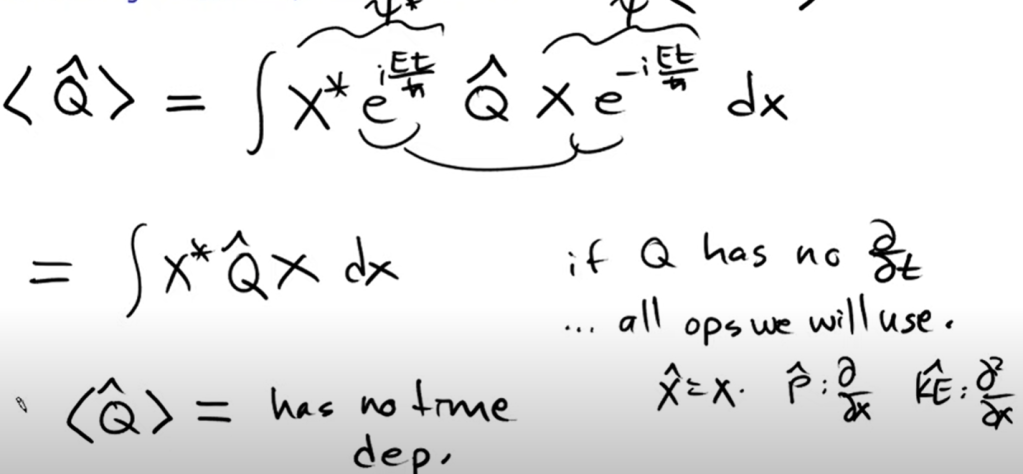
So for time independent time series part of Schrodinger Equation,

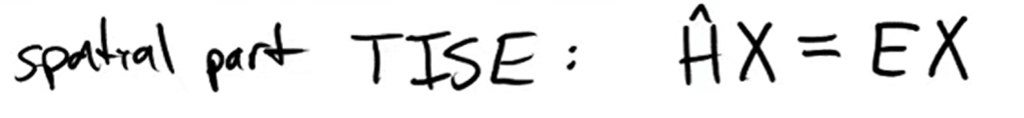
From below deduction, we learn that the Hamilton Operator expected value is related to the energy

and there is no uncertainty in this energy value.

We say Hamilton operator is a Hermitian Operator, so what is Hermitian operator? It’s to take conjugate and transpose, and the end outcome is same as the beginning.

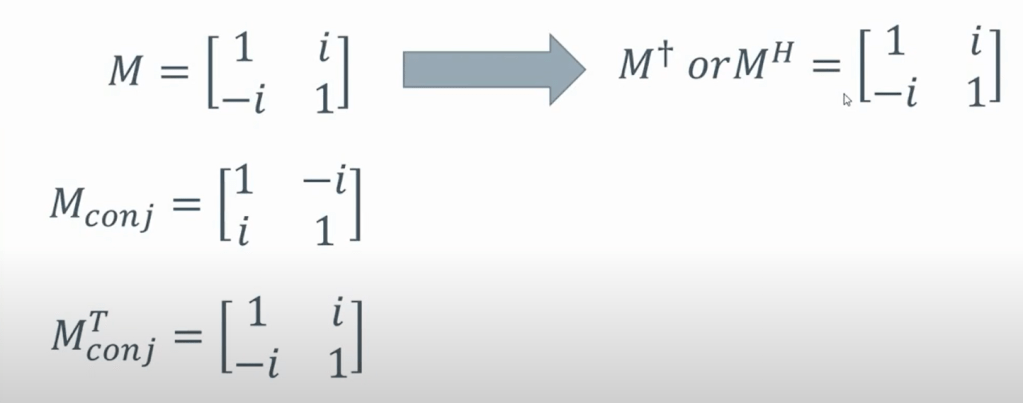
So Hermitian Matrices/Operators always have real eigenvalues.