Geometry can be very intuitive and ingenuine to solve problems, yet applying linear algebra in a tedious way is more thorough and systematic. For example we can try to prove a parallel’s diagonals are perpendicular if the four sides are equal: vector dot product.

It is consistent with what we know in elementary math that

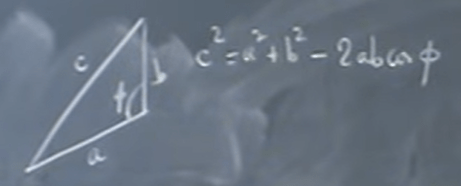
So it naturally leads to the famous Cauchy-Schwarz theorem, how to prove it? Professor Shifrin’s approach is not intuitive to me at first glance, so here I laid it out per his lecture:

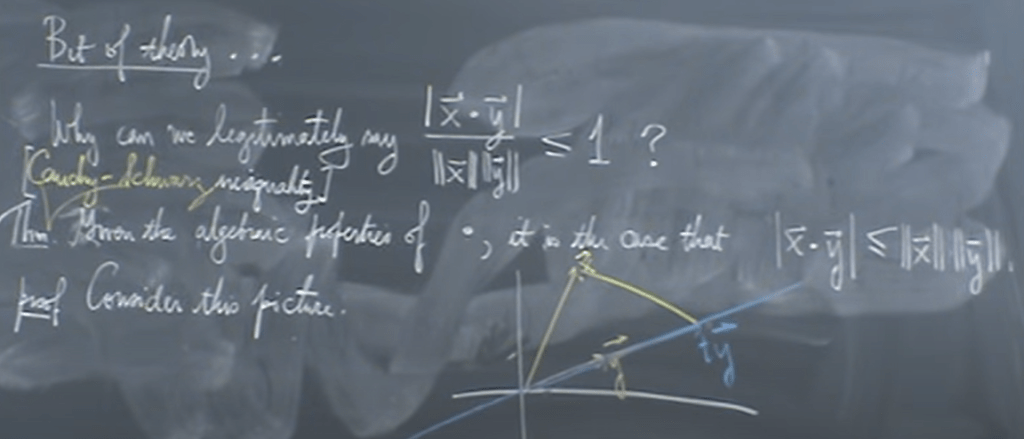
The purpose is to find the t on y vector line so the distance between x vector and ty is the minimal, in math form it is

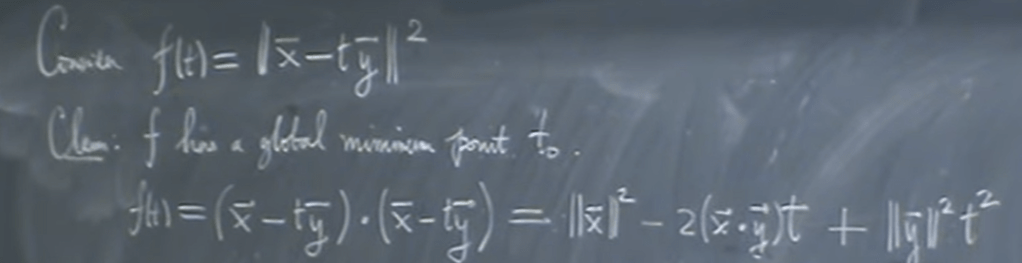
How to find the t, even we can apply geometrical knowledge by drawing graph and figure out the convex is the point t0, linear algebra prefers – and it will pay off in long run – take derivative to compute as

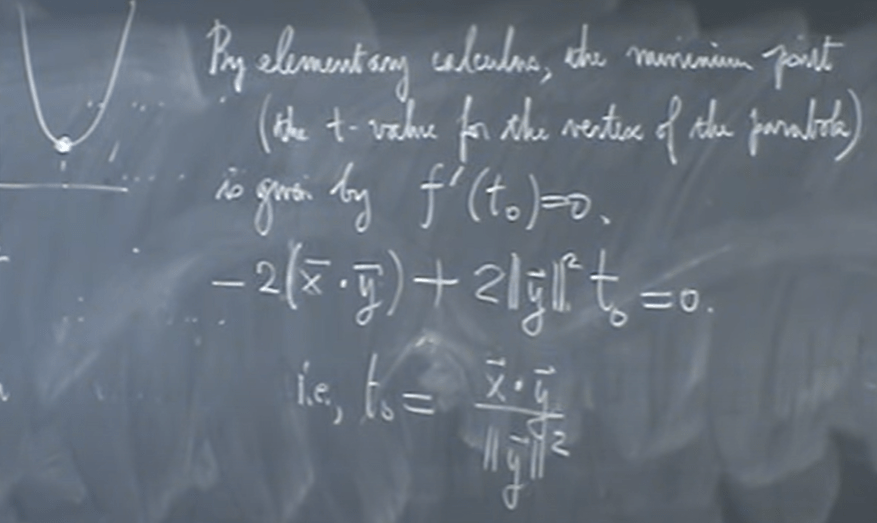
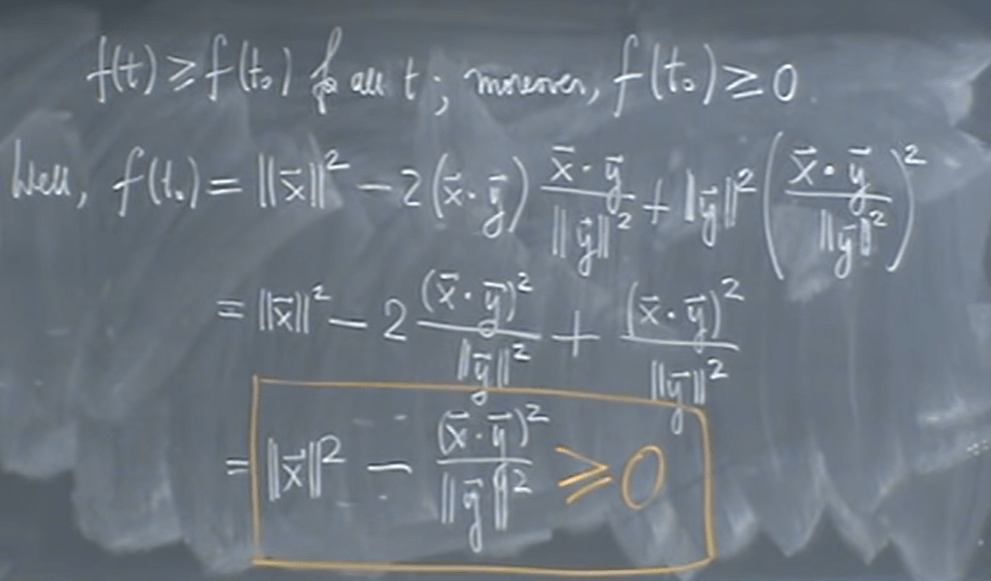
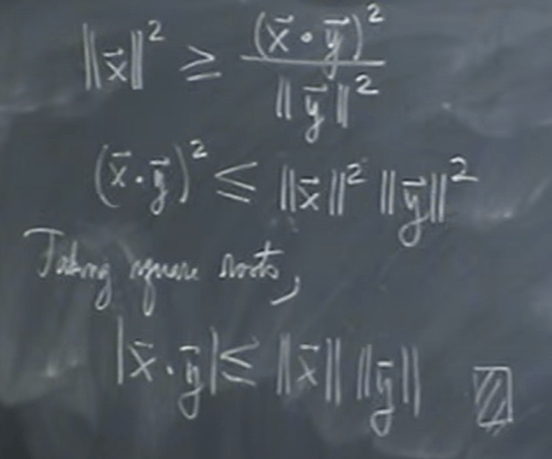
It seems to be such a simple fact, yet requires such rigorous proof, and what’s more, there are a broad scheme of applications such as triangle inequality. Here is how prof. Shifrin proves “triangle inequality” using Cauchy theorem.

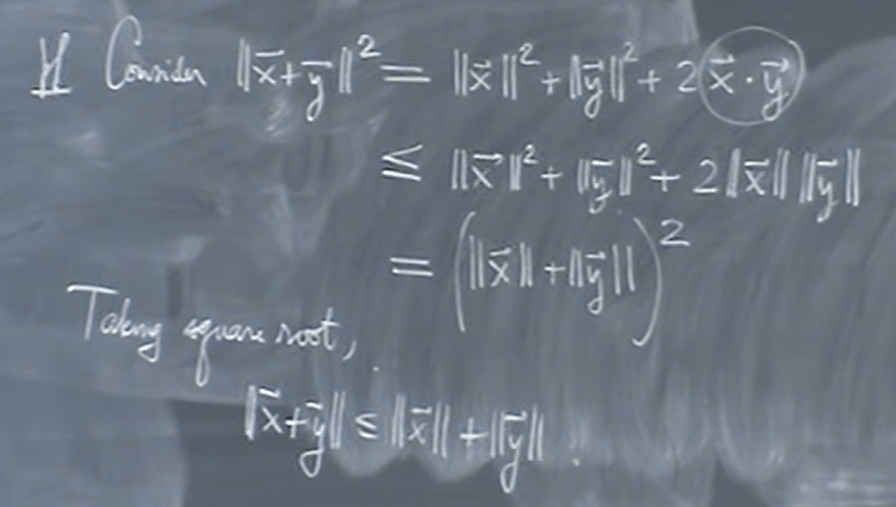
Finally prof. Shifrin left a homework as below, instead of goring through from scratch as he demoed, mathematicians tends to be more clever to apply proved theorems in this case Cauchy’s to directly prove further theorems. And minus in math in essence is same as plus,

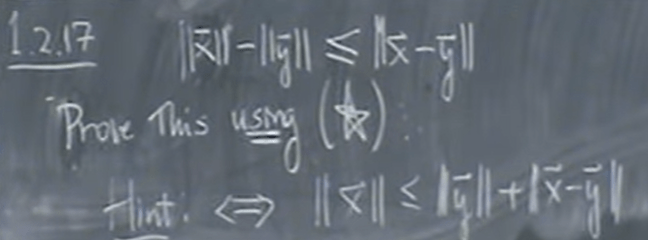
Hence, || X|| = || X – Y + Y ||, which is <= ||Y|| + || X – Y ||, end of proving.