So Prof.Shifrin gives the lecture on Linear Mapping on a systematic way that streamline pieces here and there I collected along the way. It’s absolutely beautiful.
First, what’s the definition of linear function/linear mapping? according to wiki, in mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping. between two vector spaces that preserves the operations of vector addition and scalar multiplication. that’s consistent to the definition of subspace.

Generally, as graphed above, we need to judge if a T(transformation/function) that takes variable in Rn to project to Rm is a linear mapping or not? We check by adding and scaling, and see if these operations are preserved before and after transformation. A typical and simple example is that T(X) = X + 1, it doesn’t hold, because if we scale it by 2, T(2X) = 2X + 1 != 2(T(x)) i.e. 2X + 2.
Next, given a good understanding of LM, ask yourself, what is a good example of LM: R2 –> R2? One answer is rotation by theta degree:
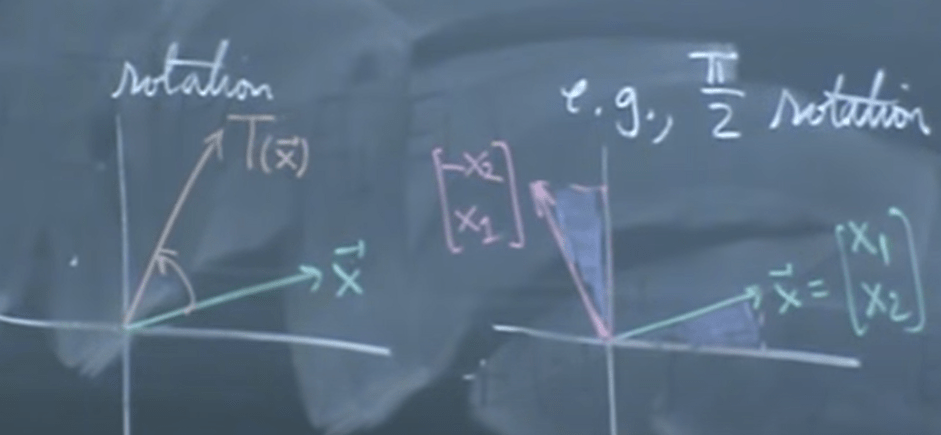
So this below transformation expression is the rotation by 90 degree counter clock-wise and is linear:
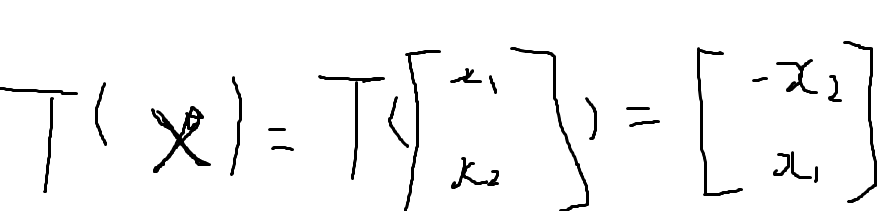
Now we explore Rn –> Rm, we know this transformation of LM can be written in Matrix (m by n) format, where n is the column number. Also we know any vector can be expressed as composition of a real value and standard basic vector e:


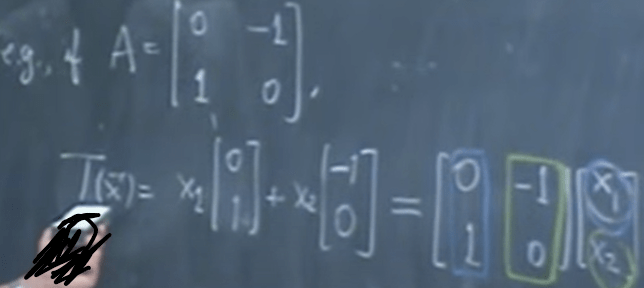
Arriving to the form in the right part, conversely, given the right part (matrix times a vector, more often we encounter), we know it’s laid out like in the left side – column time row element x1, x2, … now practice:
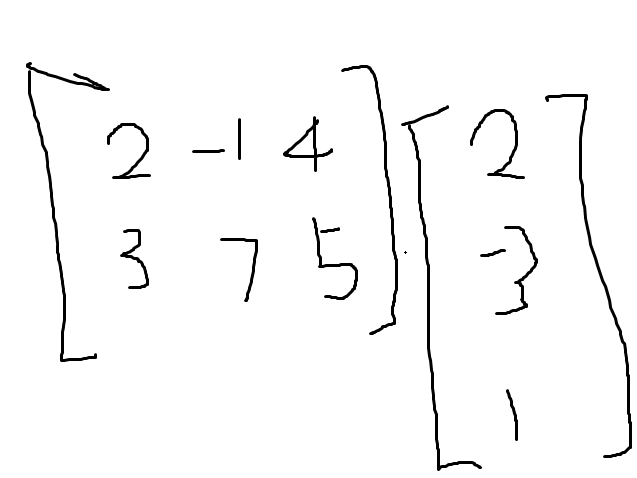

It’s extremely powerful/quick to compute when certain columns are zeros:
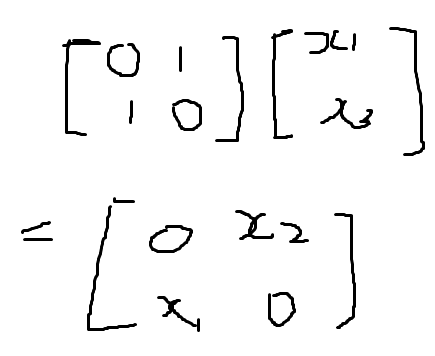
Generalizing it, a matrix A can be thought of as linear combination of component of vector x times a1… an; or it can be thought of as row vector of A dot product vector x.

Try a HW problem applying Linear Mapping knowledge:
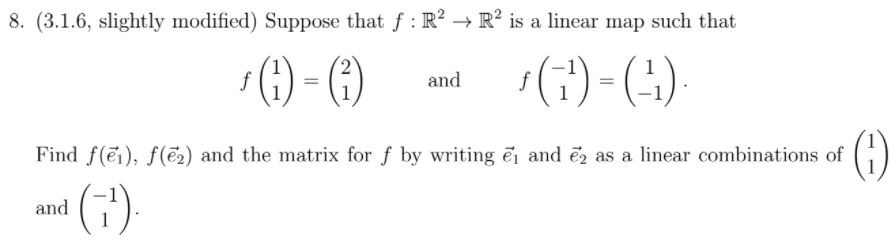
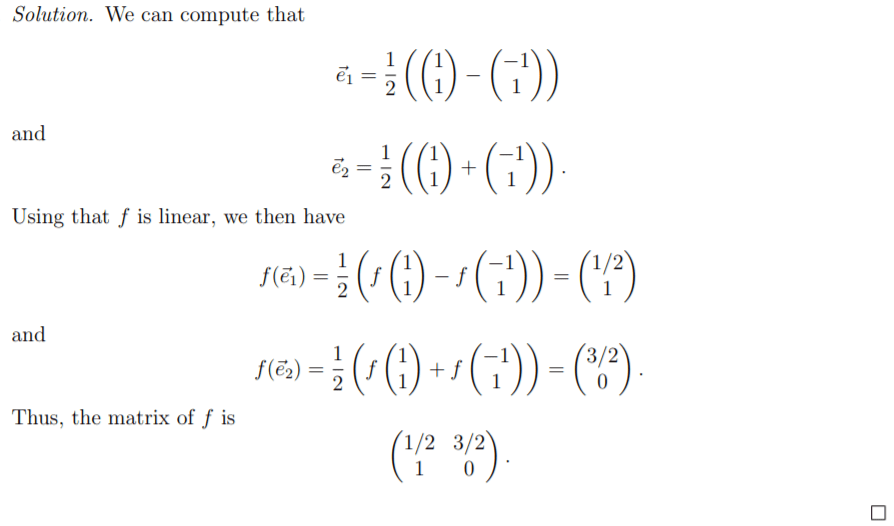
this is not intuitive, there got to be a better way to solve