Prof.Shifrin provided a comprehensive yet brand new perspective to understand inverse, transpose, and cross product in matrices.

First, the concept of identity matrix is needed which makes A time it to be still A:

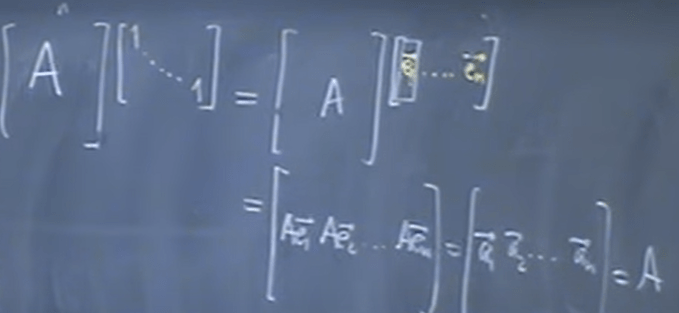
Transpose is to just swap position diagonally, but there is one caveat we raise and it’s just identified here that the one by one matrix is equivalent to the scaler.

AB transpose is to transpose B and then A, reversely. The other professor has more intuitive explanation there. Derived from this, we get

This is very useful and can be applied in real life problems such as combining various ingredients to make cookies.

Next to understand determinant, why do mathematician came up with such a notion. Let’s start with a generic form

If ad-bc != 0, then the inverse of the generic matrix on the left side is valid.

If ad-bc = 0, it’s equivalent to saying the vector [a, c] and vector [b, d] are parallel:

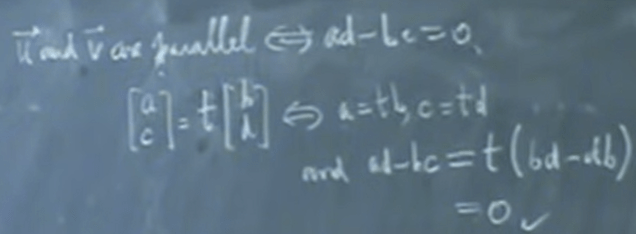
Now if we assume ad-bc not zero, then spam of two vector u and v denoted as such can be visualized

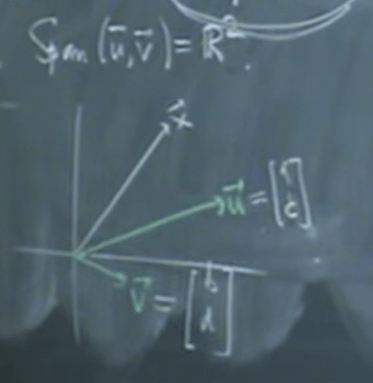
Then to interpret in geometrical way,

And to make it convenient, mathematicians come up with the name “determinant”, called it det(A) = |a1..an|. Once definition is given, certain properties can be inferred:

Addition on how to compute inverse of a matrix, use an HW example:

Expressed as product of elementary matrixes are

Ask the question to learn more about “inverse”/”invertible”: