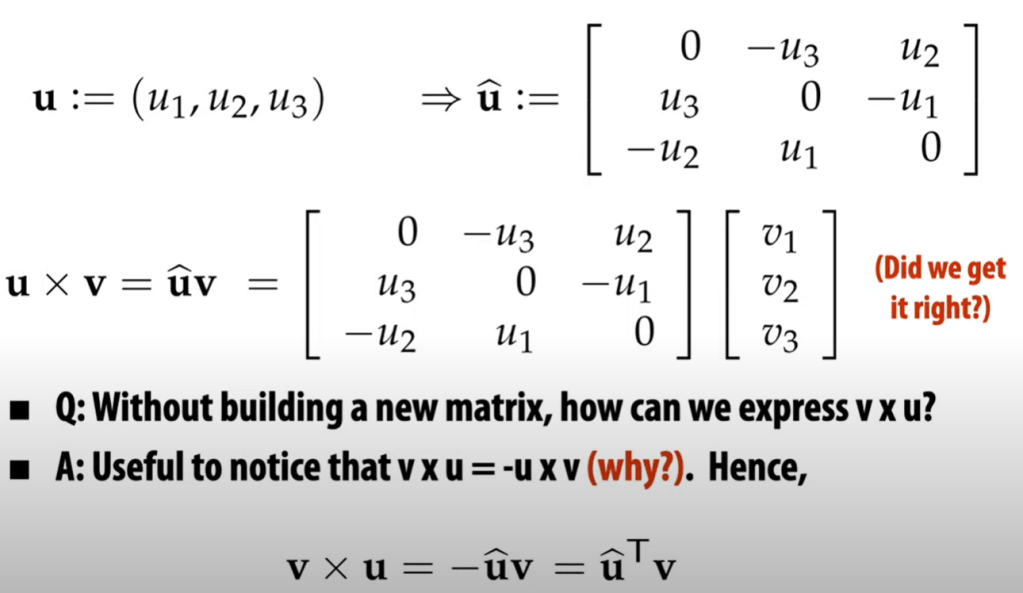Systematic Review Cross Product

It’s been iterated multiple times of what cross product is and how useful it is in math and physics. But Prof.Shifrin’s version is still quite mind-blowing.

He starts from the determinant formula for an R3 matrix:

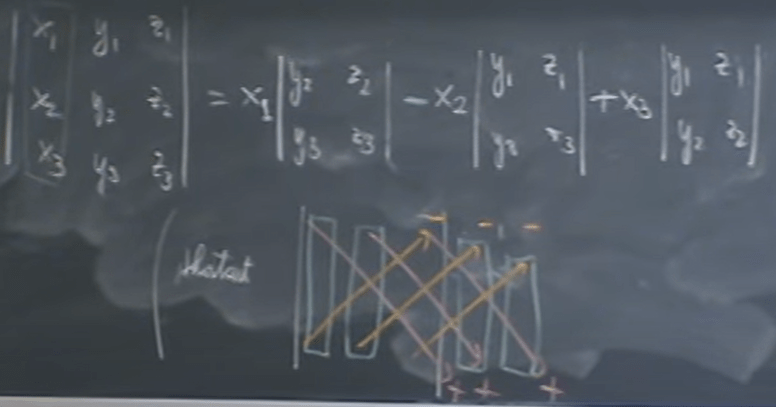
Then he switched to discuss the properties of determinant of R3 matrix

And give the definition of cross product of two vector u, v living in R3 as

(note cross product only applicable in R3)

Using a real example, we found a vector u dot the cross product of u and v gets zero, does it hold always?

**an additional vector z dot to cross of u and v is equivalent to the determinant of z, u, v.** hence it’s easy to prove the above one example holds generally due to the **determinant properties**.

Based on this definition, we wonder what is the direction/sign of cross product and what is the magnitude? This is the best part of prof. Shifrin’s lecture on this topic!

Here is his deducting process:

properties of determinant, in conjunction of above definition of cross product equivalent to the determinant, we get the magnitude of u cross v squared is the determinant, geometrically, we can continue to the below cube graph

this volume is equal to determinant, equal to the magnitude of cross product squared

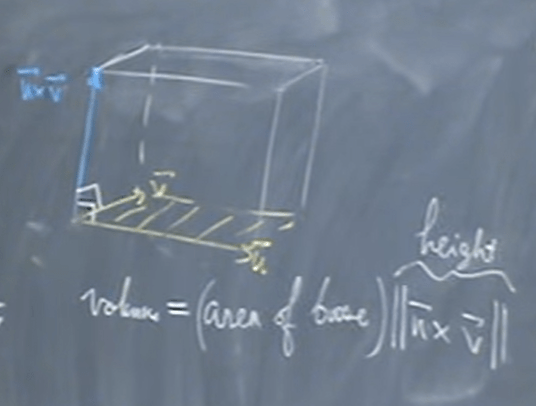
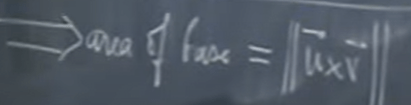
Hence we get the magnitude of u cross v is the area of the base

Grasping this concept help think differently and quickly on solving math problems. For example, given V spanning the two vectors given below, we’d express in below form of V plane leveraging the orthogonal vector A.

A is simple the cross product of the two vectors:

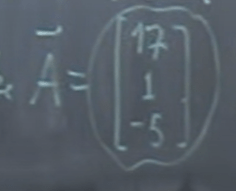
that’s how we express plane in math more generally

“Determinant” is a very profound concept in math. There are multiple ways to understand. One is above, adding another one from Keena Crane at CMU on teaching computer graphics:

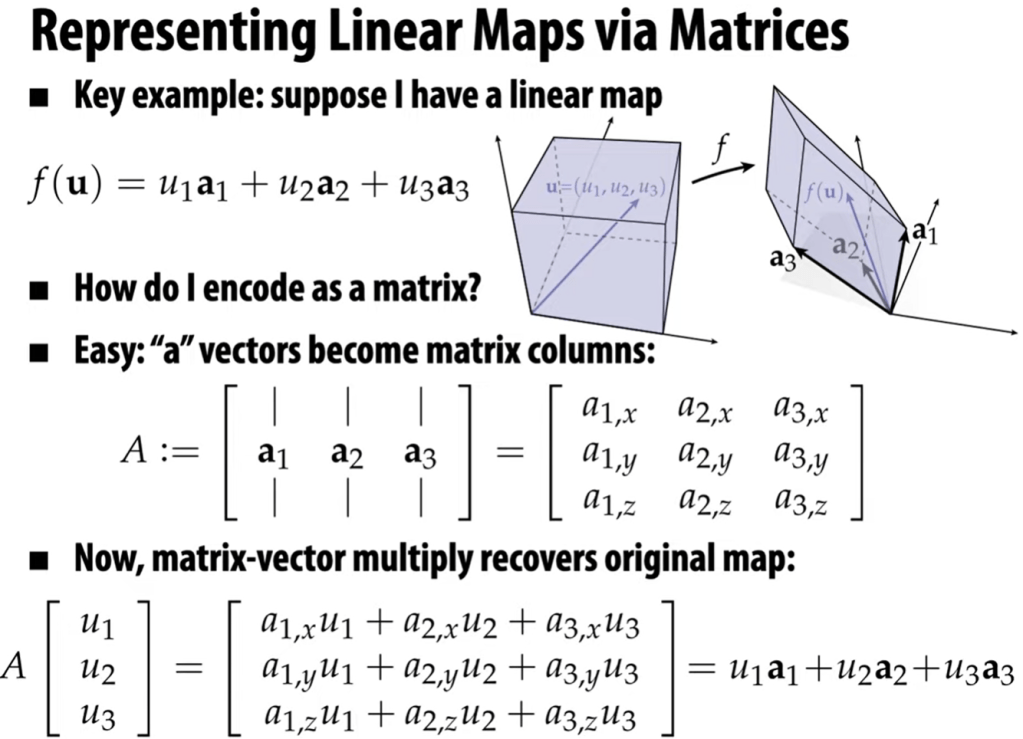
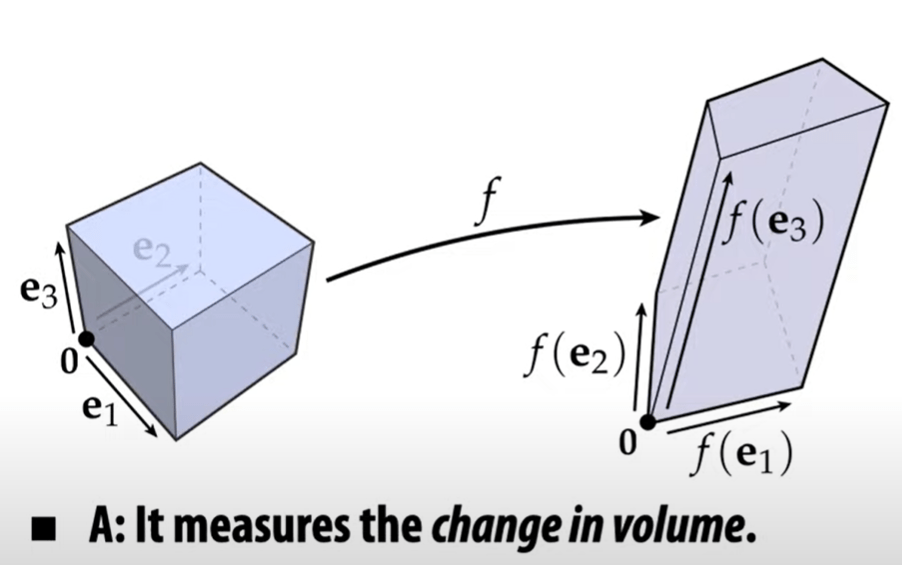
So apparently here you can determinant is the volume of three vector object. However, what is the determinant of a linear map/matrix? It boils down to our understanding of matrix first visually or geometrically as below: