Commonly starting with R2->R like geo location with altitude, longitude and point to a temperature scalar value. If we fix one variable, either longitude or altitude, we define partial derivative as follows:

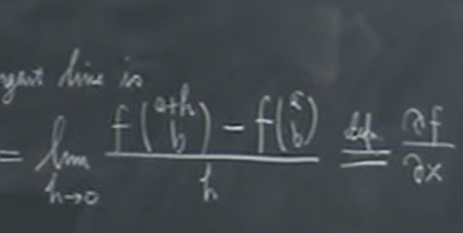
Now we throw in a bit complex real example

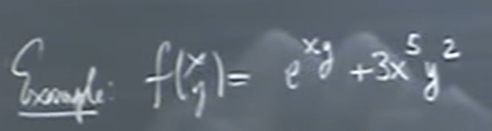
We can write out the partial derivative say on x, fixing y as

Here is another example:

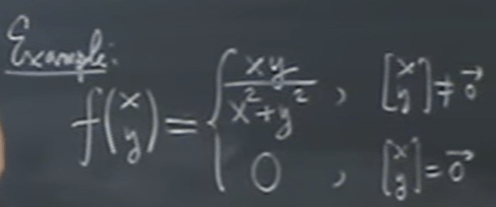
This is tricky when asked to find the derivative at origin zero. If setting y fixed, moving along x axis or y axis.

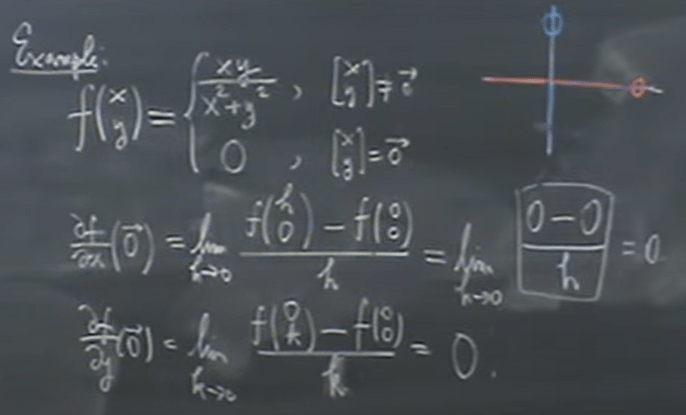
If move from a line y = mx,

This is surprising because there are partial derivatives on origin point, but apparently the function is not continuous on that point. What works in one-variable calculus ceases working now.

Generalizing form only x, or y axis moving, we name a random vector v to move along, we use a succinct symbol below to denote the derivative in the direction of v of function f at point a:

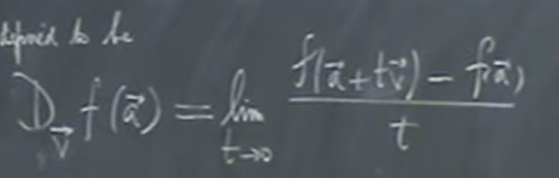
Applying this concept using the previous example:

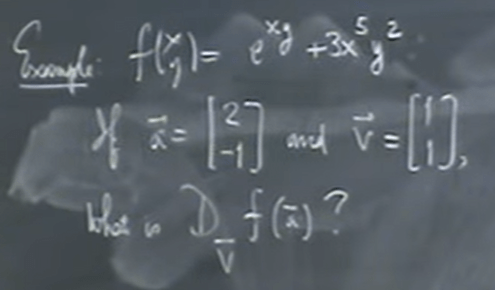
According to the definition, if we literally follow and plug in as

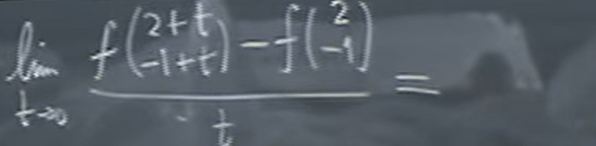
The outlay is incredibly complex to proceed. So a very clever way is to see intuitively that function of parameterized function pfai

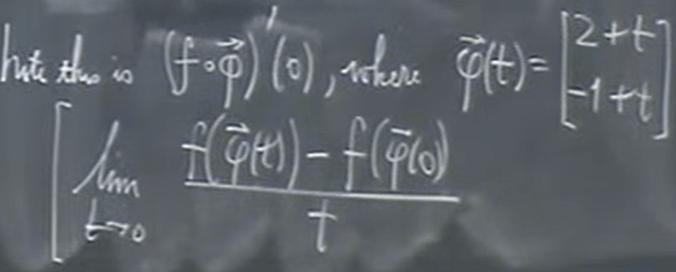
So taking the limit of above equation is equivalent to take derivative of f(psai(t)) at t=0, which is

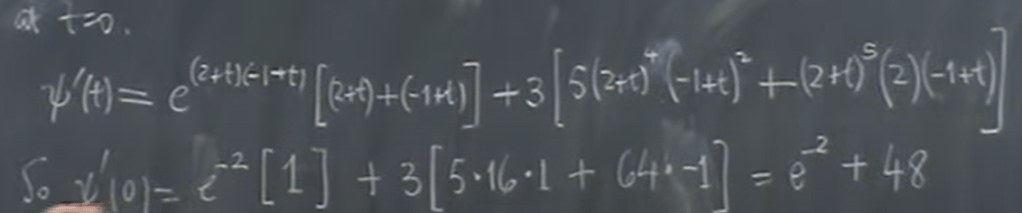
Lastly, prof.Shifrin pointed out what if the v vector is doubled, that means the D we just calculated is also doubled, but common sense we know the slope is not doubled, hence we need to differentiate “slope” and “rate of change” in this Directional Derivative. for Slope we should always define the directional vector a “unit” vector!

Now let’s take a look at this example, which already know that it’s not continuous at origin, the question to ask now is does it have directional derivative at origin?

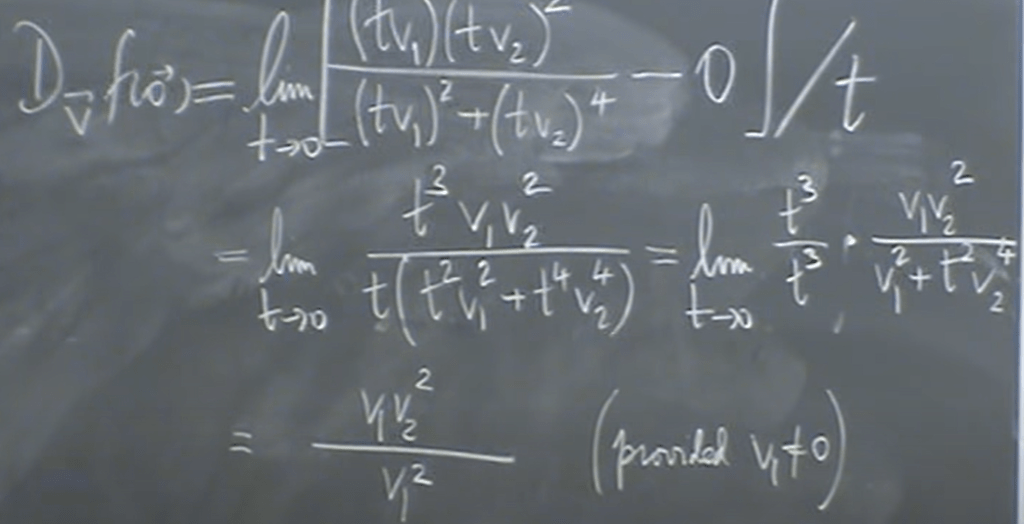
But we know this function’s derivative at x or y axis direction at point O is zero. How to picturize it?

The reason mathematicians love to use derivative/slope/tangent line to approximate a function, is that the error (per h) decrease the most:

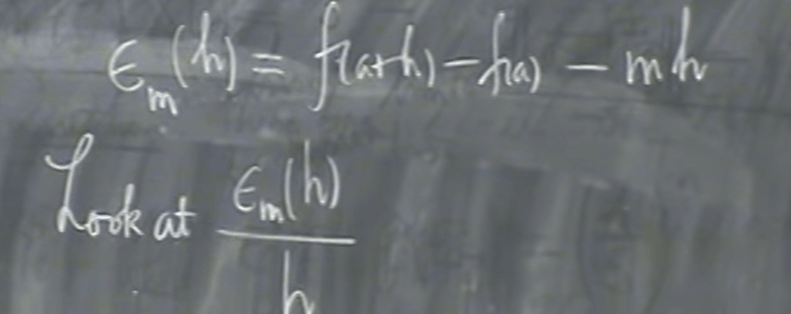
Now using math language to describe the problem: suppose f maps a neighborhood of a in Rm to Rn, we say f is differentiable at a if there is a best linear approximation to f, that is a linear map T, mapping Rn to Rm, so that

This T is called the derivative of f at a, the directional derivative.

We say f is differentiable is

To remove the abstractness and see it in a real example, previous example:

Added on Nov2021 to go over derivative matrix concept by using the hw from Xiaotian math:

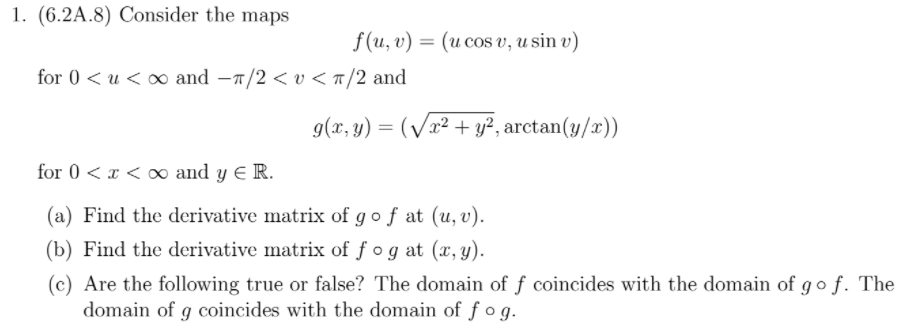
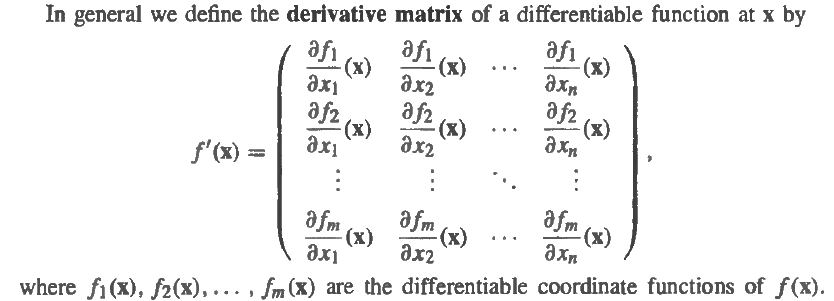
from HW#6

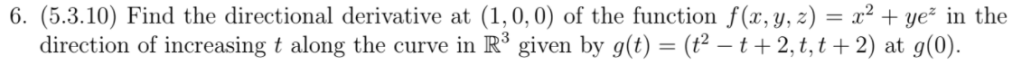
How to compute Directional derivative such as the canonical problem above?

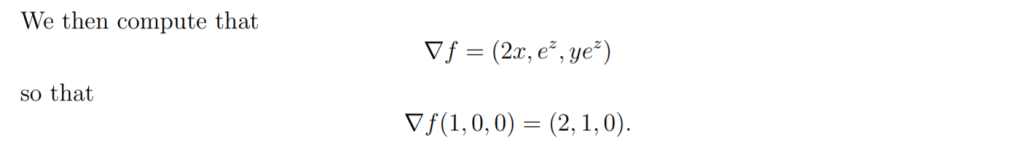
This is from

Let’s deduce it:

Intuitively it’s easy to see, gradient is normal to the tangent plane on the point of the graph, direction defined by a vector u or v may have an angle to the normal, so the dot product/cos angle part is the effective directional derivative.