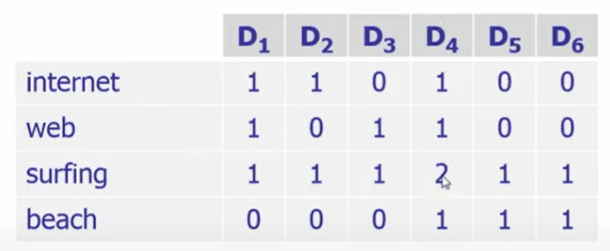
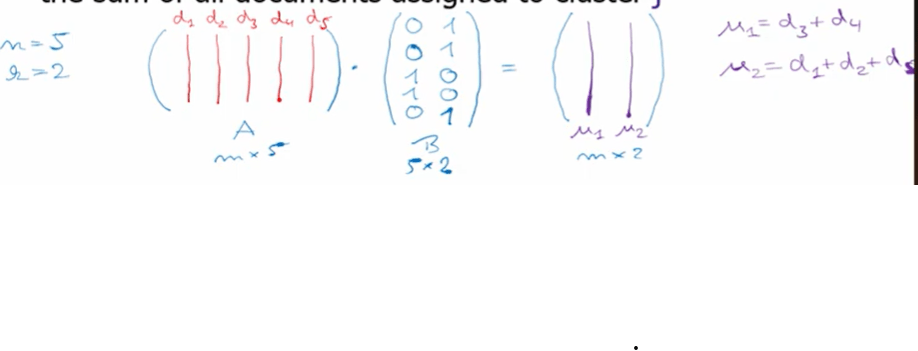In IR area, documents always are represented in vector form and organized in this standard way:

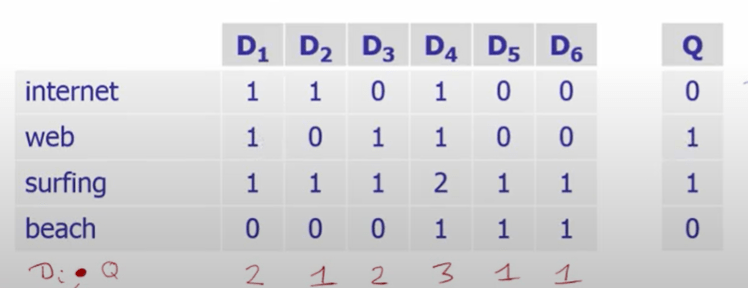
So if we have a query composed of two words “web” and “surfing”, querying it across this term-document matrix is basically Di dot q on each column,

which can also be expressed mathematically as q^t dot D

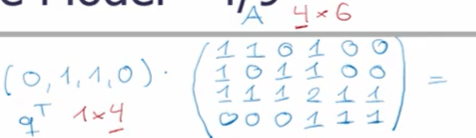
The way three three values are organized exactly reflect the inverted index format

Clustering is a simple concept, in which you compute RSS

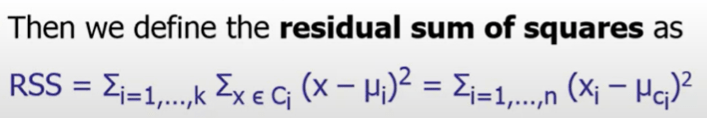
K-Means’ basic idea is to find a local optimum of the RSS by greedily minimizing it in every step. This is a linear computation as shown

How to choose k, we introduce lambda as a turning parameter RSS + lambda * k

K-means works well for compact clusters, but not for scenarios such as below

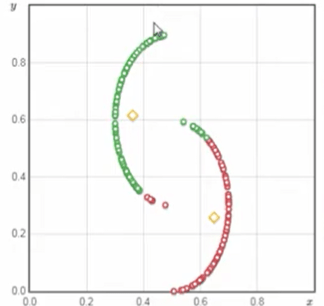
Or for this

It’s worth to know the alternatives:

What we often care is the distance of the documents, Euclid distance between two vectors can be expressed as

The computation can go hairy fair quickly if we apply the formula rigidly, but after applying the simple trick as described above, leveraging that the x and y normalized value is 1, the problem will be diminished to dot product between x and y, which are sparse matrices. The math can be laid out as

A is the term-document matrix mX5, and B is the two centroid matrix form composed by two centroids, each represented as document vector, the matrix operation leads to miu1 and miu2, since all is at the same scale, we even don’t need to normalize them to compute the average K-means on these two centroids.