There is a web called freebase is so far the largest open general-purpose knowledge base to date. It’s now taken over by Wikidata, as is stated in its front page “the free knowledge base with 95,839,953 data items that anyone can edit.”

It’s worth noting to compare it to the “semantic web”, which makes machine easy to process info on any website without applying NLP by leveraging structured info in html format.

SPARQL is the standard query language for KB, SPARQL Protocol And RDF Query Language. An example is

Moving on to NLP, NLP problems can be categorized as
POS(Part of Speech) Tagging: for each word in a sentence, determine whether it’s a noun, a verb, a preposition
Name-Entity Recognition: recognize words in the text that refer to entities from a given knowledge base
Sentence Parsing: given a sentence, compute its grammatical structure, usually based on POS tags
Semantic Role Labeling: deeper semantic analysis of given sentence, e.g. the subject and object of the verb

First, POS tags, there are 36 such POS tags, for example

It’s proved that using the mathematical approach (Markov Chain…) 97% of accuracy can be achieve, pretty comparable to human experts. So let’s dive into the math.

A most simple Markov chain is to predict the mood shown as

Now bringing it to new level, assume there is a hidden state of whether one sleeps well or not, which affects the mood the next day.

Now comes to the math tricky part to find the hidden state

The algorithm to solve this likelihood(MLE) problem is Viterbi Algorithm.

So to solve the maximizing problem, we are aiming to solve a recursive problem as

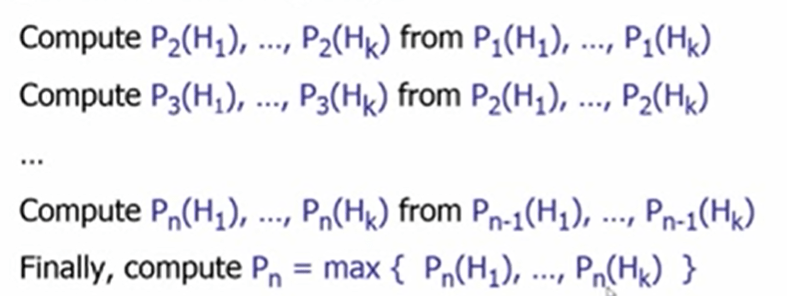
Tensorflow has a hiddenmarkovmodel built for it.

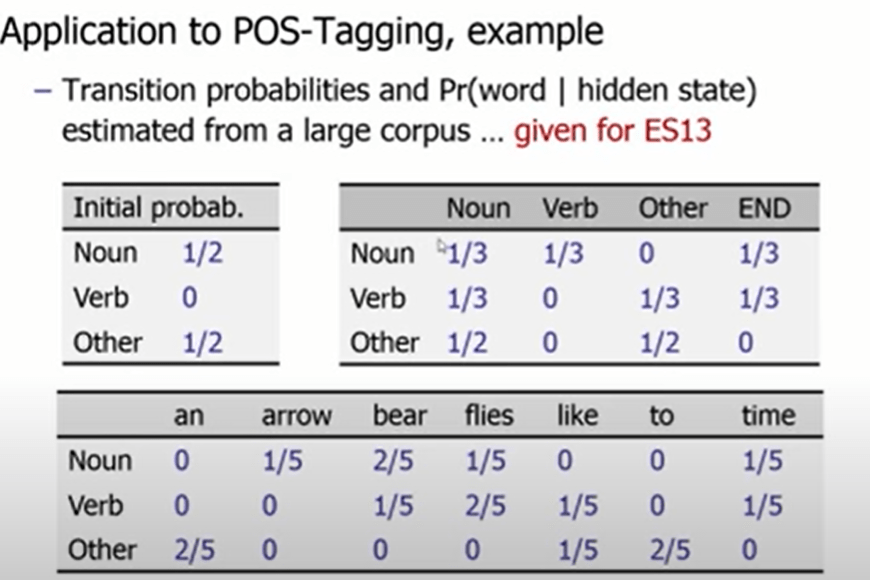
Now we will apply this algorithm to POS tagging by a toy example:

The example sentence is “time flies like an arrow”, the observed states is the sequence of words, hidden states are the sequence of POS-tags.

import numpy as np

# States (Hidden)
states = ["Sunny", "Rainy"]

# Observations
observations = ["Umbrella", "No Umbrella"]

# Transition Probabilities: P(Next State | Current State)
transition_probs = {
    "Sunny": {"Sunny": 0.7, "Rainy": 0.3},
    "Rainy": {"Sunny": 0.4, "Rainy": 0.6},
}

# Emission Probabilities: P(Observation | State)
emission_probs = {
    "Sunny": {"Umbrella": 0.1, "No Umbrella": 0.9},
    "Rainy": {"Umbrella": 0.8, "No Umbrella": 0.2},
}

# Initial Probabilities
start_probs = {"Sunny": 0.6, "Rainy": 0.4}

# Given Observation Sequence
obs_seq = ["Umbrella", "Umbrella", "Umbrella"]

# Number of states & time steps
num_states = len(states)
num_obs = len(obs_seq)

# Viterbi Table (for probabilities)
viterbi = np.zeros((num_states, num_obs))

# Path Table (to track backpointers)
path = np.zeros((num_states, num_obs), dtype=int)

# Initialize base cases (t=0)
for s in range(num_states):
    state = states[s]
    viterbi[s, 0] = start_probs[state] * emission_probs[state][obs_seq[0]]

# Fill the Viterbi Table
for t in range(1, num_obs):
    for s in range(num_states):
        state = states[s]
        max_prob, best_prev_state = max(
            (viterbi[prev_s, t-1] * transition_probs[states[prev_s]][state], prev_s)
            for prev_s in range(num_states)
        )
        viterbi[s, t] = max_prob * emission_probs[state][obs_seq[t]]
        path[s, t] = best_prev_state

# Backtracking to find the best sequence
best_last_state = np.argmax(viterbi[:, -1])
best_path = [best_last_state]

for t in range(num_obs - 1, 0, -1):
    best_path.insert(0, path[best_last_state, t])
    best_last_state = path[best_last_state, t]

# Convert indexes to state names
best_state_sequence = [states[i] for i in best_path]

# Print results
print(f"Most likely state sequence: {best_state_sequence}")