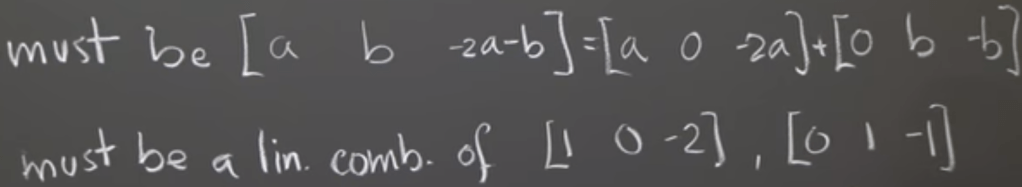Connecting all the dots, this is the heart of LA, by Dr.Grang at MIT 18.06

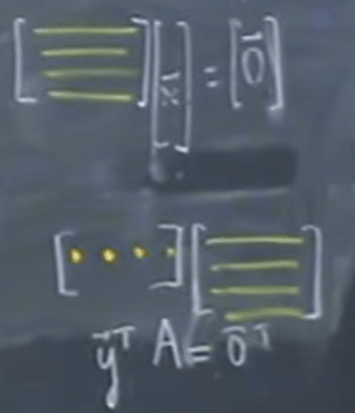
The fourth space is null space of A transpose, also called left null space.

problem solving can be tricky if not proficient. for example, given Ax and its solution as in below screenshot, you should infer that A is 3 x 3 matrix, dimension of the null space is 2. Then how to reverse engineer the A? use column operation!

to be added more later!, here you are: eyeballing A, first column + second column leads to 0, hence [1, 1, 0], the third column is zero, hence [0,0,1]; reversely, if you are given [0, 0, 1], meaning the third column is zero all, given [1, 1, 0] meaning first column plus second column is zero, first column is the already deduced to be [1, 2, 1] hence the output is [-1, -2, -1].

Try to continue on this series, but there is no such content so created a new blog for it. It’s from Prof.Shifrin again.

First, be extremely familiar with the row operation and column operation:

column operation put the vector x on the right side, so each row times the column, it is extended from the original elementary equations, so linear composition of x[] + y[] +… (seems confusing here); row operation puts row vector on the left side.

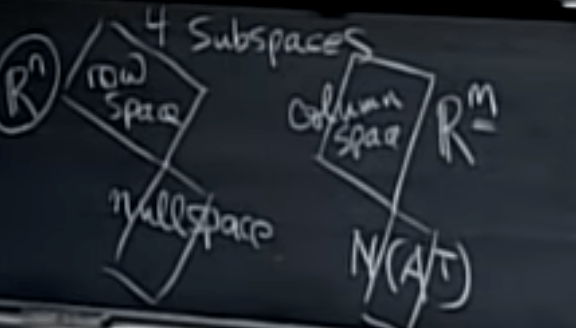
So there are these four fundamental subspaces:

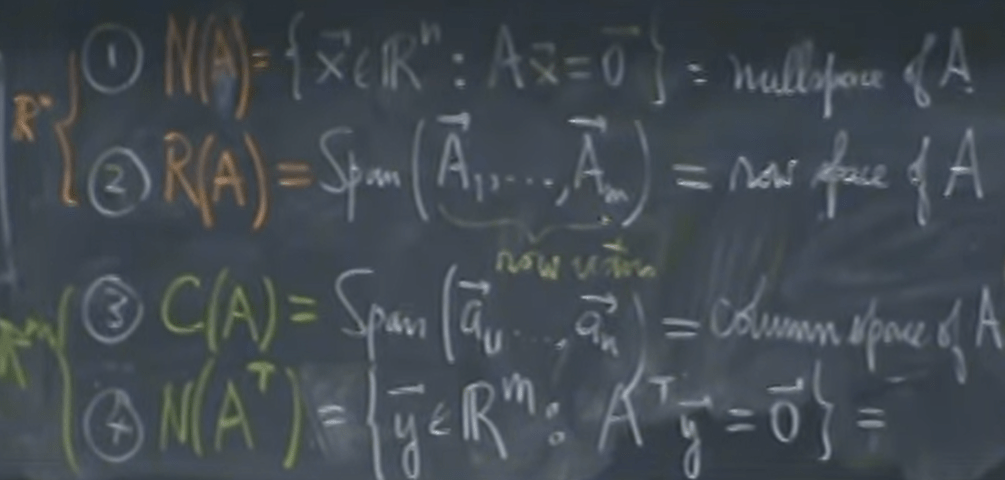
He goes on to prove that rank of R(A)=C(A)=Rank of A.

More insight with an example, for a matrix A, practice the method to find the Null space of A,

We wrote it as

so x2, x4 and x5 are free variables, so we can make them 0. ? …

The pivot columns of original A gives basis.

Here is a practice problem:

refer to this link for answer.

Another practice on matrix space:

the TA has a trick in solving this problem