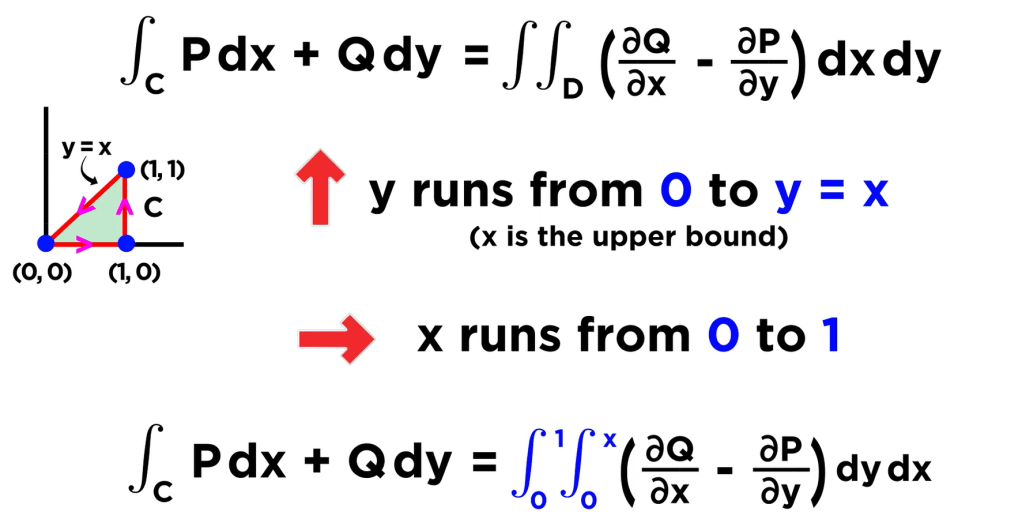HW10#1&2 is to plot vector field so you get a fast intuition about abstract symbols of vector field equations. Note graphically, a vector field is conservative if it has no tendency to “swirl around.” If it did swirl, then the value of the line integral would be path dependent. A conservative vector field has the direction of its vectors more or less evenly distributed. 

Examples of conservative:

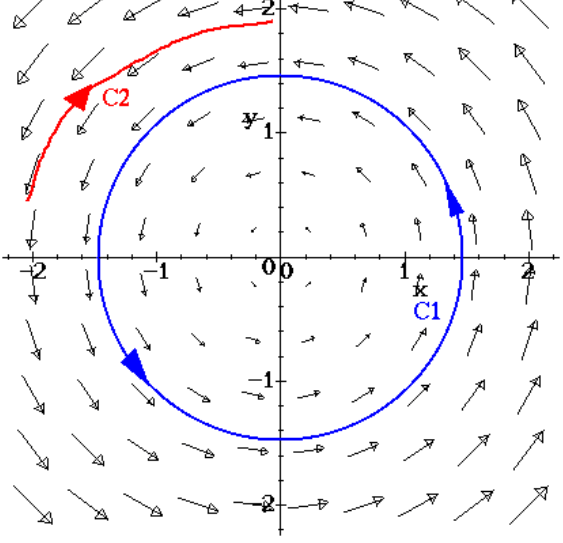
What about F=(-y,x), it swirls, so you can not find the reverse function:

What about F=(y,x), if you calculate the reverse function f(x,y) = xy, if calculate per Clairaut’s theorem, partial M to partial y = partial N to partial x = 1, so it’s conservative, however according to Wolframalpha, it seems swirl(? need to be confirmed later on)

Problem #4

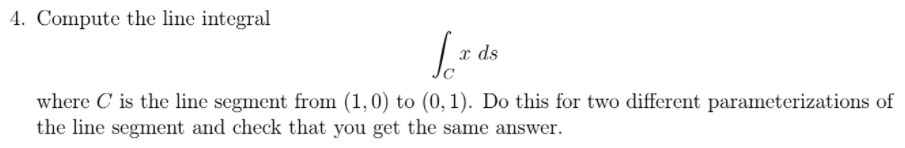
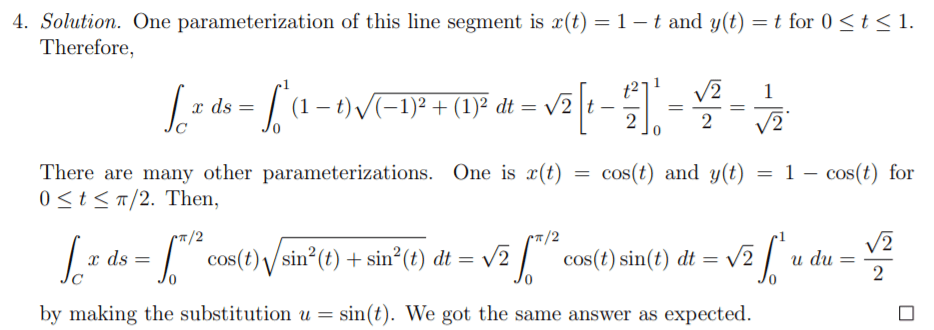
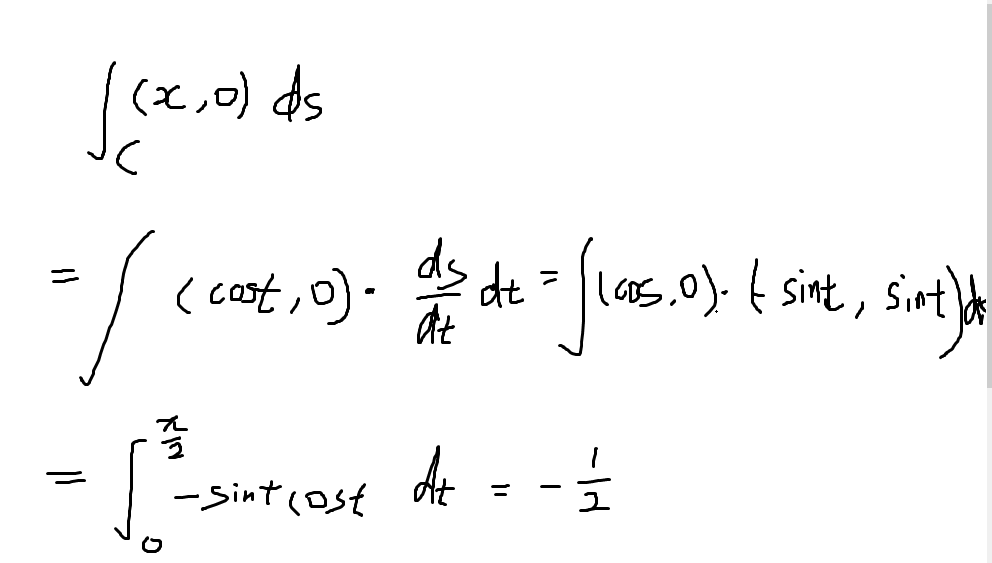
Conceptual understanding of line integral, which can be analyzed on two situations: LI on a scalar field or on a vector field. If on a scalar field, it’s exactly like to calculate surface area, volume; if on a vector field, it’s to compute the work of vector such as a Force on a path.

In this problem #4, the to-be-integrated part is written as x, indicating it’s a scalar. If we write it as

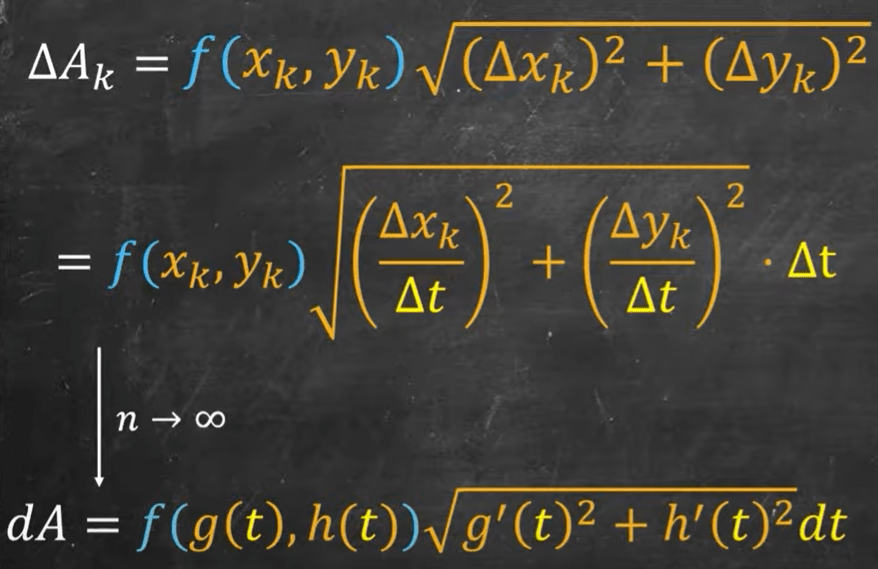
The last problem’s key is to be able to draw out the octant and set the t(angle upward) as the parameter

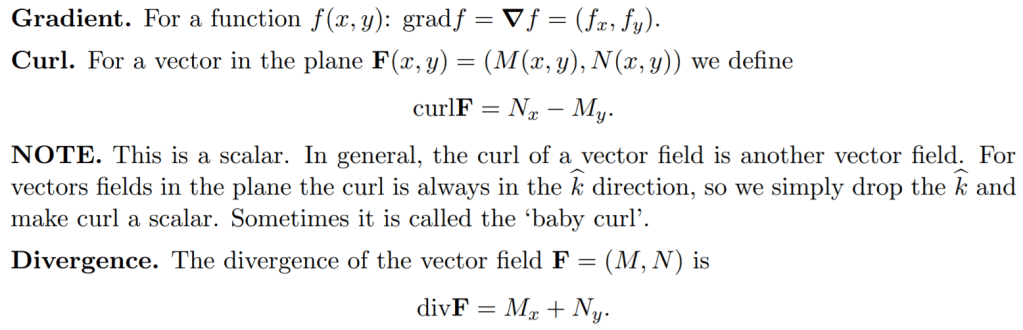
There is this he fundamental theorem of gradient field, which is defined as

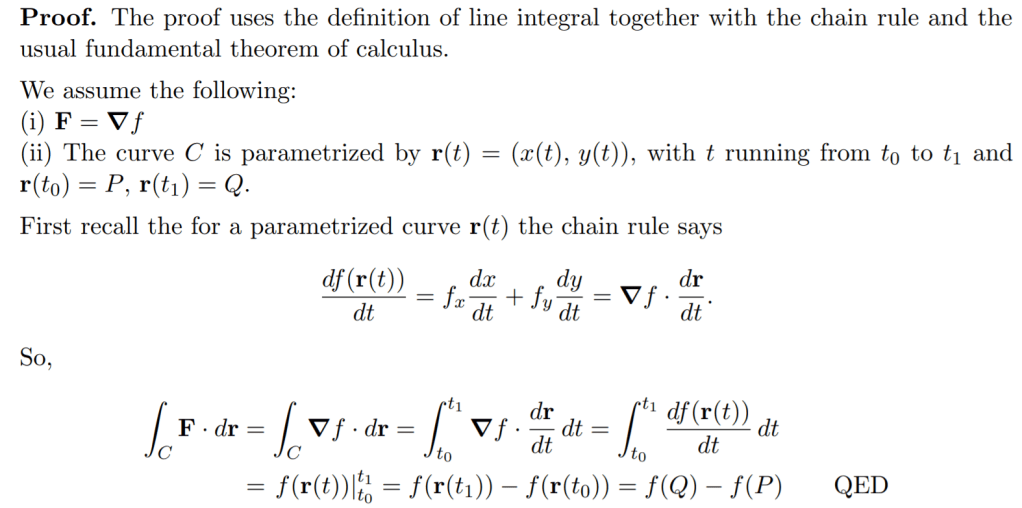
HW#4

first, to check if it’s closed and smooth and simple, yes it is

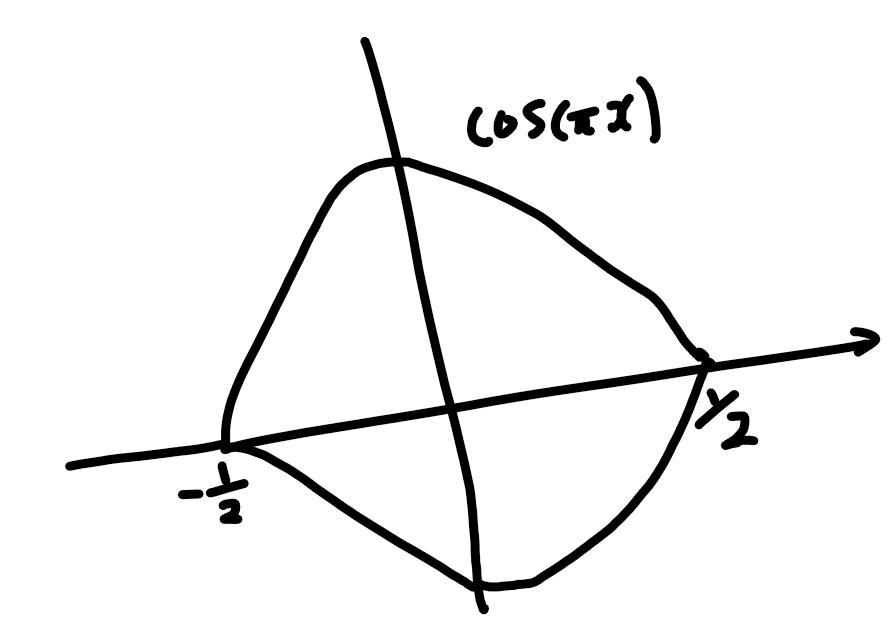
second, try to tackle the problem using Green Theorem, there are two difficulties: 1. even the y boundary is expressed simply by one function =cos(piex), x part is broken into two parts, so it’s hard to compute, why don’t we also break them into two closed curve and integral one by one? 2. the P and Q have x square and y square on the denominator, it’s hard to compute derivative, so why don’t we convert/parameterize since you can spot it looks like a pseudo-circle.

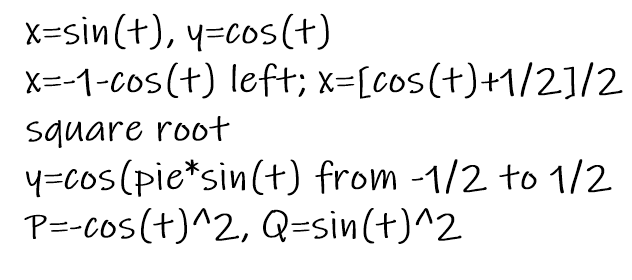
Note the Green theorem is a little tricky in applying dx and dy boundary. for example in Dr.Trefor’s video, a simple square is used

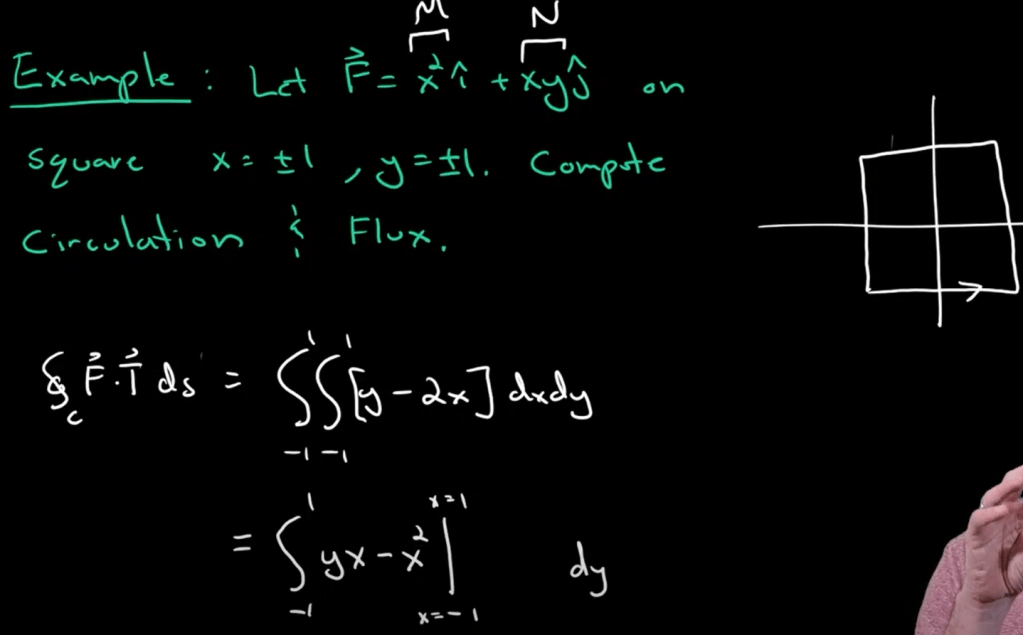
What is the square is not centered around the origin, what if it is a triangle instead of a square? the solution for the triangle is as below