To have myself in making robots, there are Foundation Courses: Mechanics, Controls, Perception, Artificial
Intelligence, and Human-Robot Interaction (HRI). I tapped on Mechanics and Controls offered by Steven Brunton.

This blog is to document his fabulous explanation on control system, applying the eigen vector and eigen values in linear algebra. To start, a simple control system such as moving pendulum can be expressed in

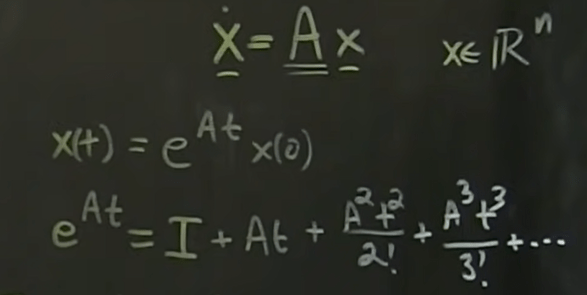
This power series is good but too cumbersome to handle and not possible to analyze further, hence, mathematicians always resort to linearly independent eigen vector and eigen values to tackle. Here matrix A can be

so AT = TD.

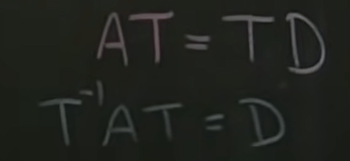
The key idea is that to analyze x transformed by A is difficult, but if we express X = Tz, using T matrix (transposed vector composed of eigen vectors) to multiply z(in z coordinates in the eigen vector direction), we get x too.

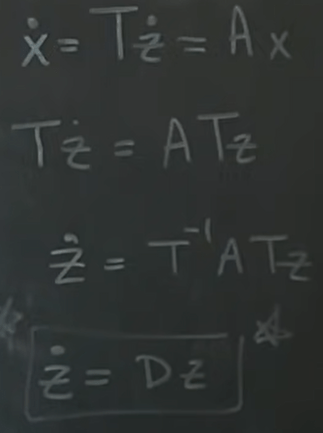
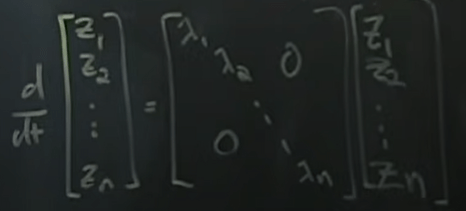
Then the solution is so much easier because it’s in orthonormal (independent or decoupled) coordinates, clean and concise way to compute. Here is how.

Since AT = TD, so A = TDT^-1

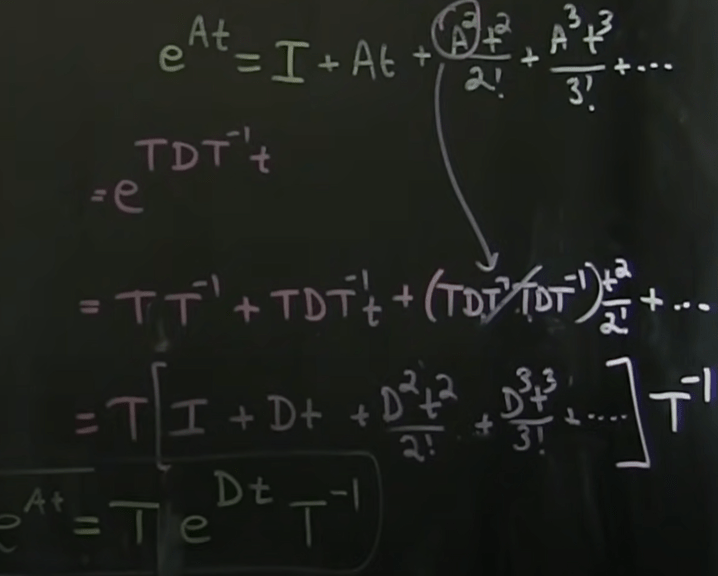
Hence, the original solution (which we are very familiar with) now can be expressed as follows:

So we just need to plug in computer package(python or matlab) to quickly get D (eigen value in diagonal) and T(eigen vectors), the solution is complete.

After writing down above, I still feel something is not 100% crystal clear, so I need to apply the key points in my “problem solving” summary to continue digging. The key points are “A vital point I want to emphasize here is “details” or “sensitivity” or “observing really closely”!

In this problem, the concept of z is not crystal clear. It is the transformed version of x, i.e.. x = Tz ! T is derived/computed from the matrix A. As written above, it’s a matrix (composed of eigen vectors). In all, the reason to go through that trouble using new matrix T is to have linearly-dependent, convoluted x and A to be expressed in decoupled coordinate system. It’s consistent to Fourier Transform!