The common or familiar way to solve ODEs are to separate variables and apply integral factors, it can shape into Bernoulli Equations which looks like below with same line of thinking.

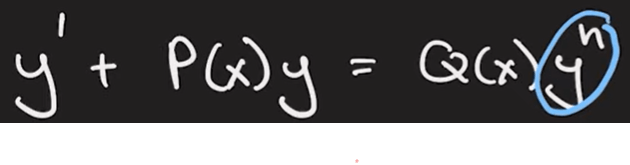
Later on, Laplace transform is introduced to transform higher order derivatives into simple algebraic equations.

This session provided by Dr. Trefor is mind blowing, it is to use infinite/power series to solve ODEs.

The main thinking is like following: any value(represented by variable x) can be represented in series form:

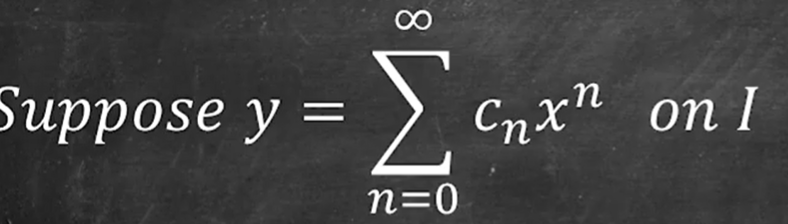
refresh memory on the Taylor’s power series, so the derivative of y is

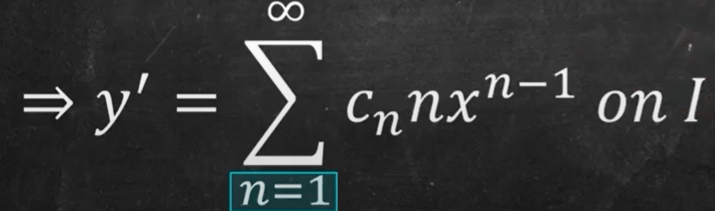
To solve the simplest ODE y’=y,

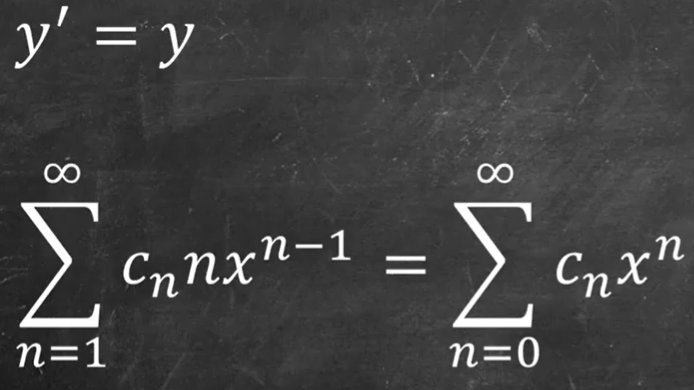
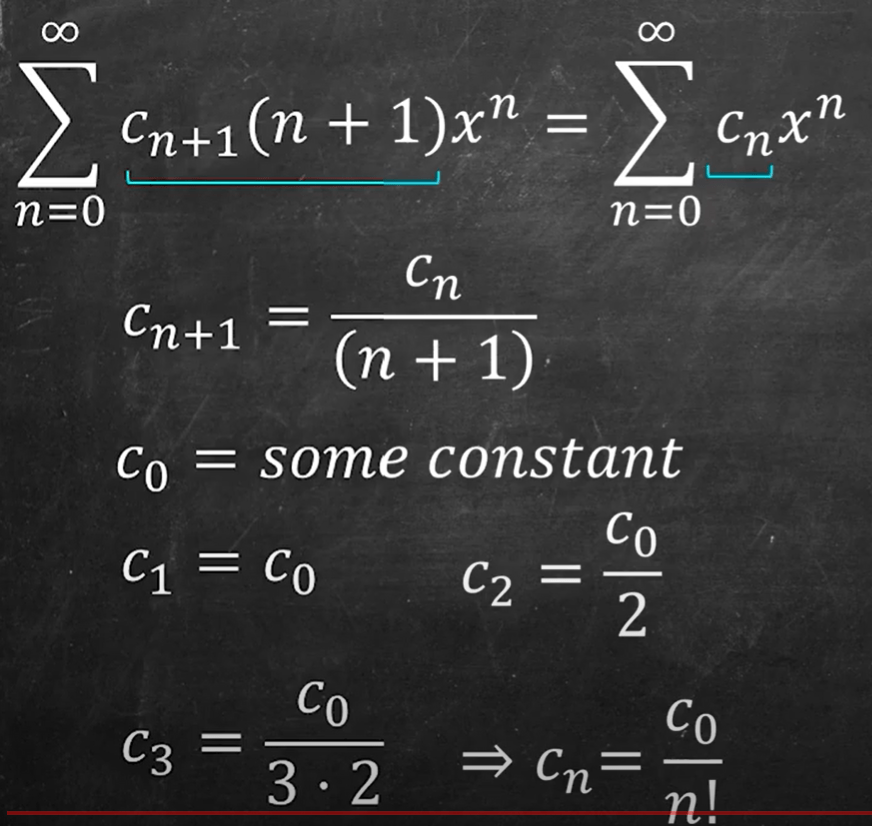
Be mindful the premise is that the series is convergenable, which is tested by Ratio test. Simiraly, solving y’-xy = 0 can apply infinite series, also can apply basis method as below

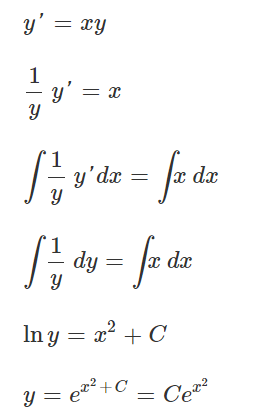
A more difficult example on applying infinite series to solve Airy’s Equation y”-xy=0.

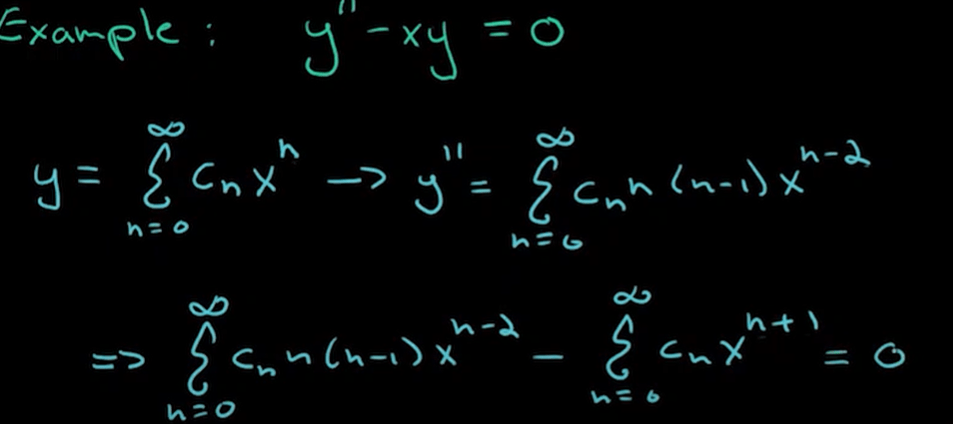
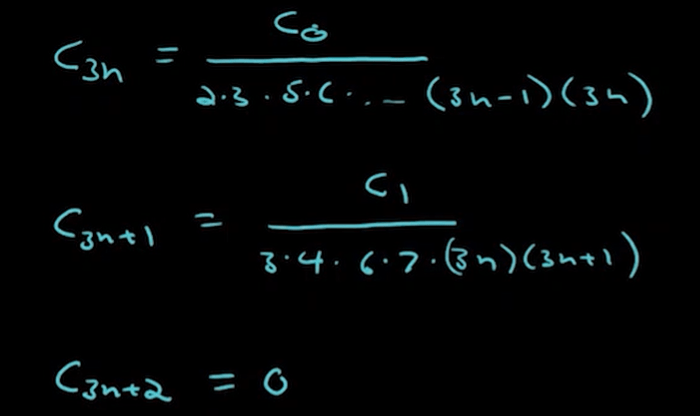
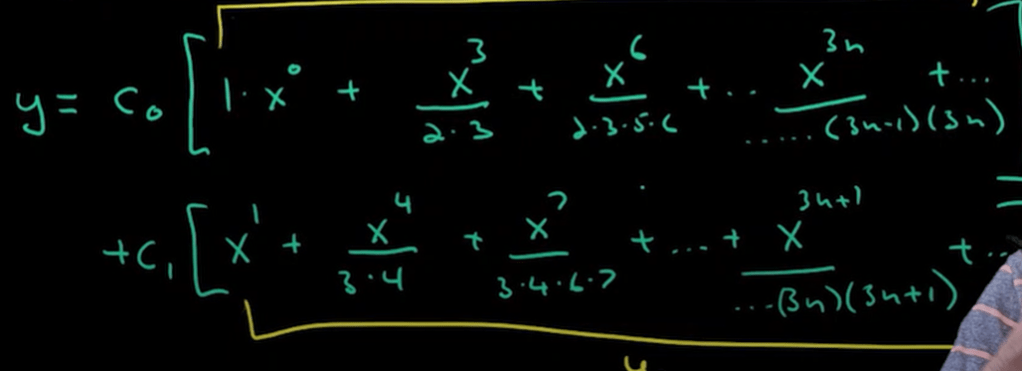
Is there approaches other than this power series to solve Airy’s equation? In Quora, there are people trying to apply Fourier Transformation to tackle it.