Masters or geniuses significantly propel the world forward. Albert Einstein, for instance, merely had to ponder briefly before effortlessly solving one of Earth’s longstanding enigmas—why rivers meander, a question that had stumped predecessors.

The quotation I refer to comes indirectly from a paper by Kent A. Bowker, with whom I deeply agree. Bowker expresses admiration for Einstein’s exceptional intellect, which few could match, and highlights his knack for distilling complex ideas into simplicity. This was often achieved through imaginative “thought experiments” and straightforward analogies.

“I begin with a little experiment which anybody can easily repeat. Imagine a flat-bottomed cup full of tea. At the bottom there are some tea leaves, which stay there because they are rather heavier than the liquid they have replaced. If the liquid is made to rotate by a spoon, the leaves will soon collect in the center of the bottom of the cup. The explanation of this phenomenon is as follows: the rotation of the liquid causes a centrifugal force to act on it. This in itself would give rise to no change in the flow of the liquid if the latter rotated like a solid body. But in the neighborhood of the walls of the cup the liquid is restrained by friction, so that the angular velocity with which it rotates is less there than in other places nearer the center. In particular, the angular velocity of rotation, and therefore the centrifugal force, will be smaller near the bottom than higher up. The result of this will be a circular movement (helical flow) of the liquid of the type illustrated in (the figure) which goes on increasing until, under the influence of ground friction, it becomes stationary. The tea leaves are swept into the center by the circular movement and act as proof of its existence.”

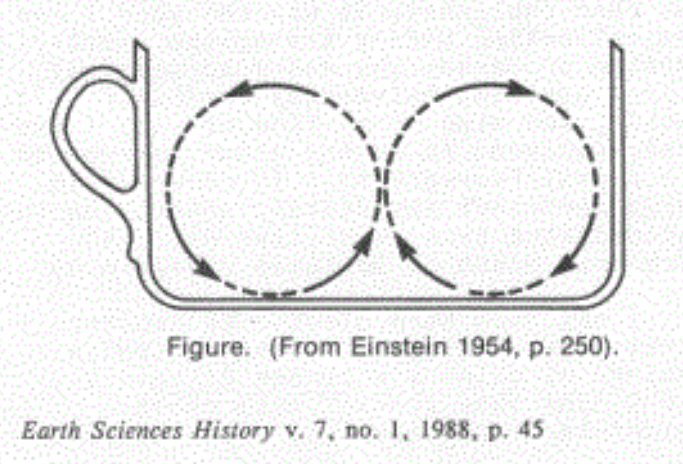
Because the higher-velocity portions of the stream will be driven to the outside(concave) portion of the river bend, erosion will greater there. And because the helical flow possesses inertia, the circulation will be at their maximum beyond the inflection of the curve. Hence the wave-form of the river will migrate in a down-current direction.