Enhanced Index Fund industry has blossomed in the 90s which can be attributed to the success of index fund and the assumption of adding a layer of active management to achieve both upsides.
Stock-based enhanced funds are typically constructed with the tools of portfolio optimization, choosing stock positions so as to maximize expected returns subject to a TEV(tracking error volatility) optimization. But there are bunch of papers show that this enhanced index fund strategy has perverse effects, does seems to increase the risk profile of active managers.
But I think there are merits of enhanced or custom indexing fund, what if it’s focused on tax-exempt strategy rather than TEV?. Another major interest I look into this is to find out how TEV is applied in optimization!
Again, so far the best source reference is provided by Vijay github repo.
His approach is simple, first, compute the portfolio covariance as is in the mean/variance frontier graph. Second, minimize this portfolio covariance by adjusting the constituents’ weights.
Covariance is basic:

Covariance Matrix is:
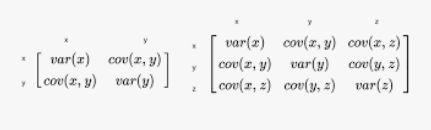
And portfolio volatility is:
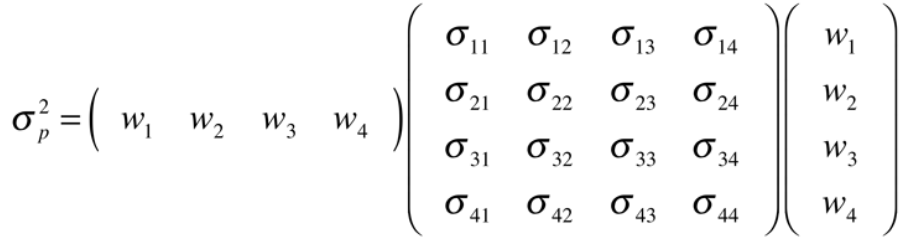
or:
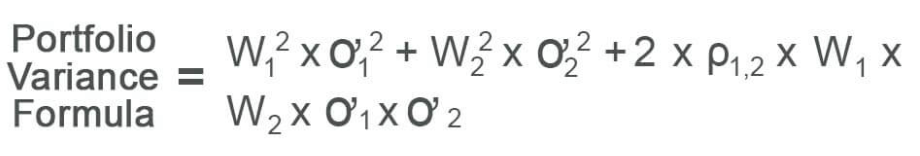
Hence there is Vijay’s optimization function as
def portfolio_vol(weights, covmat):
"""
Computes the vol of a portfolio from a covariance matrix and constituent weights
weights are a numpy array or N x 1 maxtrix and covmat is an N x N matrix
"""
return (weights.T @ covmat @ weights)**0.5
def plot_ef2(n_points, er, cov):
"""
Plots the 2-asset efficient frontier
"""
if er.shape[0] != 2 or er.shape[0] != 2:
raise ValueError("plot_ef2 can only plot 2-asset frontiers")
weights = [np.array([w, 1-w]) for w in np.linspace(0, 1, n_points)]
rets = [portfolio_return(w, er) for w in weights]
vols = [portfolio_vol(w, cov) for w in weights]
ef = pd.DataFrame({
"Returns": rets,
"Volatility": vols
})
return ef.plot.line(x="Volatility", y="Returns", style=".-")
from scipy.optimize import minimize
def minimize_vol(target_return, er, cov):
"""
Returns the optimal weights that achieve the target return
given a set of expected returns and a covariance matrix
"""
n = er.shape[0]
init_guess = np.repeat(1/n, n)
bounds = ((0.0, 1.0),) * n # an N-tuple of 2-tuples!
# construct the constraints
weights_sum_to_1 = {'type': 'eq',
'fun': lambda weights: np.sum(weights) - 1
}
return_is_target = {'type': 'eq',
'args': (er,),
'fun': lambda weights, er: target_return - portfolio_return(weights,er)
}
weights = minimize(portfolio_vol, init_guess,
args=(cov,), method='SLSQP',
options={'disp': False},
constraints=(weights_sum_to_1,return_is_target),
bounds=bounds)
return weights.x