Given I can apply the Scipy package to perform optimization, I want to understand further the math beneath it and how the algorithm of optimization is written.

Prof. Christopher Lum’s lectures are the best in explaining it. I focus on quadratic optimization instead of linear programming here. Use Rosenbrock function again:

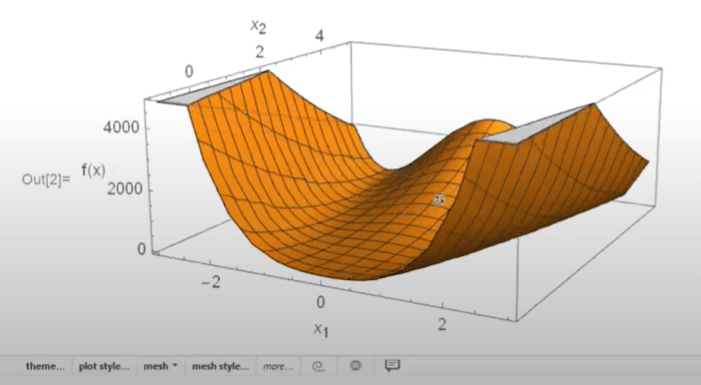
This equation can be solved analytically and we get

In matlab(there is the counterparty in scipy as is described in previous blog), fminsearch is created for this purpose: fminsearch finds the minimum of a scalar function of several variables, starting at an initial estimate. This is generally referred to as unconstrained nonlinear optimization. fminsearch uses the Nelder-Mead simplex algorithm as described in Lagarias et al. [57]. This algorithm uses a simplex of n + 1 points for n-dimensional vectors x. The algorithm first makes a simplex around the initial guess x₀ by adding 5% of each component x₀(i) to x₀, and using these n vectors as elements of the simplex in addition to x₀. (The algorithm uses 0.00025 as component i if x₀(i) = 0.) Then, the algorithm modifies the simplex repeatedly according to the following procedure.

Now we can master this numerical tool – fminsearch, next, we often times need to deal with optimization with constraints containing equality and inequality constraints:

Converting Constrained Optimization to Unconstrained Optimization, we use the Penalty Method. We use a concrete example:

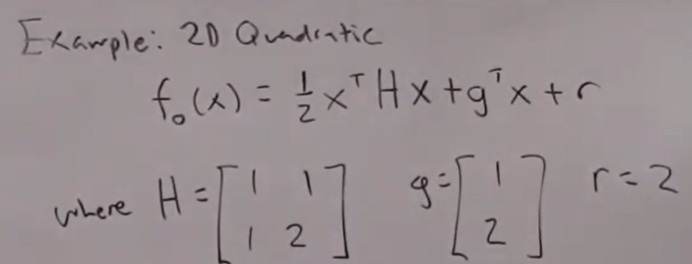
For this problem it is still feasible to replace x2 with x1 or other around to be able to analytical solve x vector. however, quickly the complexity of this kind of problem can exponentially grow that analytic solution is impossible. Here comes the genius thoughts of those brilliant mathematicians: Jensen, Paul A. and Bard, Jonathan F., “Operations Research Models and Methods,” John Wiley & Sons, 2003; Fiacco, Anothny V. and McCormick, Garth P., “Nonlinear Programming: Sequential Unconstrained Minimization Techniques,: Wiley, 1968. They come up with the approximate equation so transform the hard to tackle optimization problem into a simple quadratic unconstrainted fminsearch solvable problem:

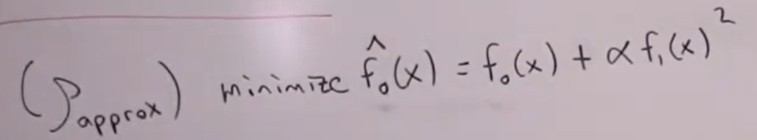
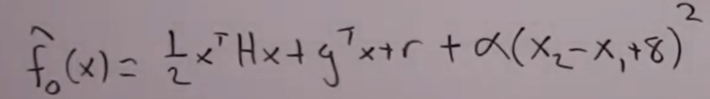
reducing down to solve gradient:

Similarly, for more equality constraints or inequality constraints, we can also transform the problem:

For inequality constraint, the penalty function for approximate equation should be:

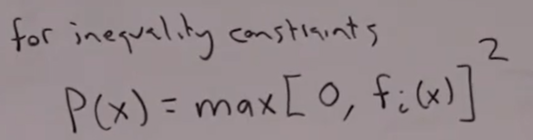
In conclusion, having both constraints – equality and inequality, the equation can be turned into unconstrainted optimization form as:

Now go back to solve the same problem with added constraints, apply fminsearch function as below: