Following Socratica’s playlist is so enjoyable to learn Abstract Algebra. Here is the link.

Why mathematicians created Abstract Algebra, because it’s very useful in all kinds of subjects. To reach to the definition, which is abstract, we start from concrete examples such as modular arithmetic, and rotating equal triangles:

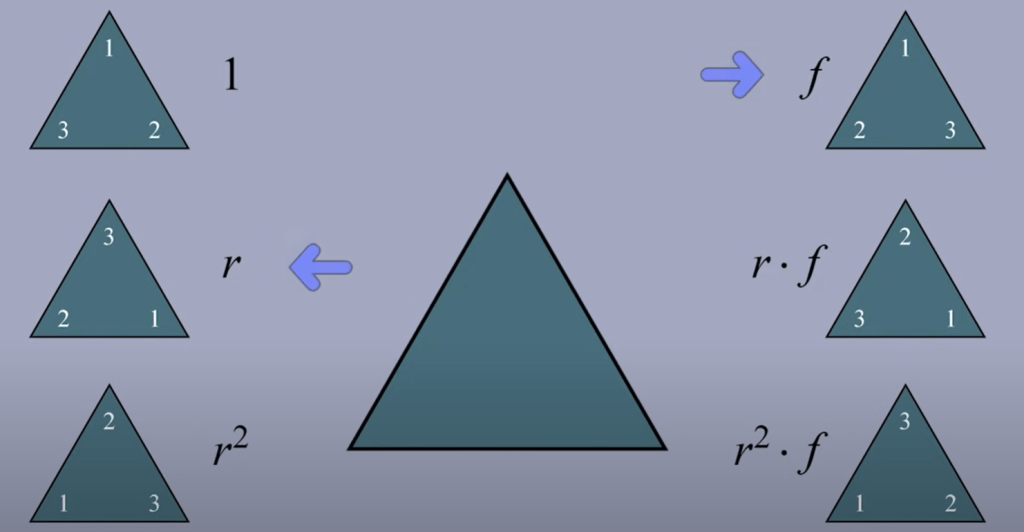
There are only two actions r(rotation) or f(flip) and entirely 6 to move triangle. We call symmetries of triangle.

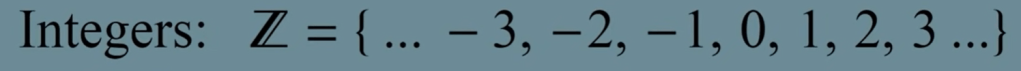
We call integers are closed under addition but not under multiplication/division.

Summarizing above three examples, there is a common property that mathematician generalized:

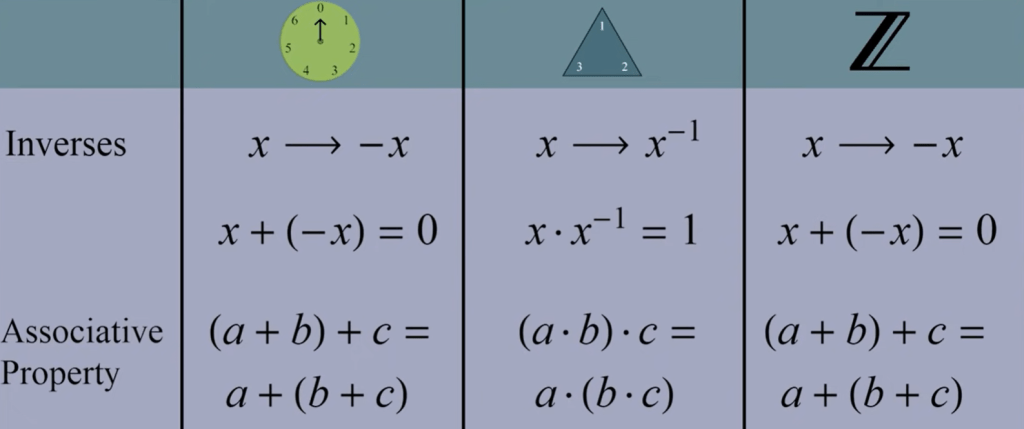
for example the inverse of 3 in clock arithmetic is 4 because 3+4 = 0 the identity, the inverse of r is r squared, the inverse of 3 in integer is -3, -3=0.

Group G is composed of a set of elements, it contains an operation, could be plus sign or multiplication sign but the meaning is not limited to plus and multiplication verbatim. Oftentimes we use asterisk. Group is closed under operation. There is an inverse exists for all element in G, and there is an identity element e. Finally they satisfy associativity.

The motivation of abstracting abstract algebra, is to solve equations in real life!