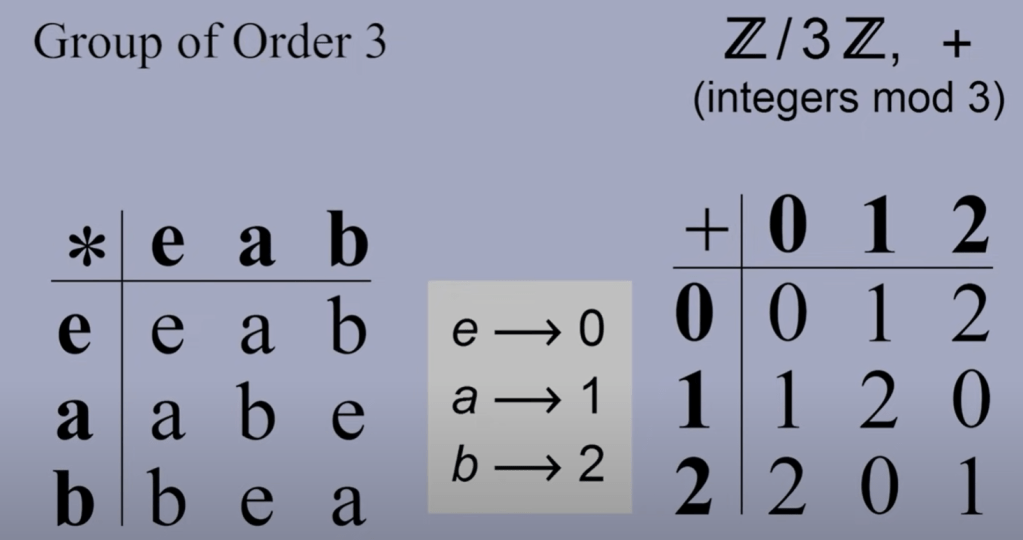
Next, we learn Cayley Tables suppose there is a group G containing these 4 elements.

So now let’s lay out the Carley tables for several groups.

First, a group of order 1 (number of elements 1)

Cosets and Lagrange’s Theorem. Here we need to grasp the concept of “Subgroup”. Here is the Lagrange’s Theorem: If subgroup H to G, then the order of H divides the order of G.

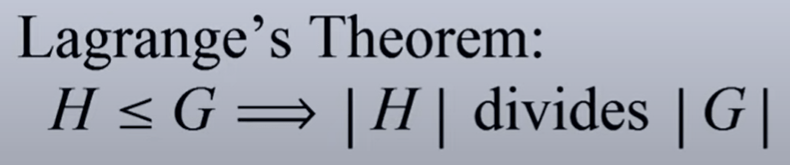
What does that mean and what’s the usage. for example, there is a group |G|=323, 323=17*19, hence according to Lagrange’s Theorem, there are 4 subgroups:

By applying rigorous logical reasoning, it’s not that difficult to deduce Lagrange’s Theorem myself. But it simply still is amazing to see how abstract math could be.

When Gauss discover modular mathematics and found great usage of this technique, the natural thought is to generalize to wider fields, thus Normal Subgroups and Quotient Groups (aka Factor Groups).

To illustrate the concept of Normal Subgroups and Quotient Groups or Factor Groups, let’s use an example:

so we can create this group called Z mod 5 composed of these 5 sets:

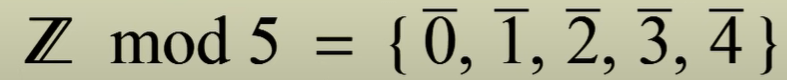
When we say a is congruent to b, that means a, b both are elements of the same set, a.k.a. has same remainder when divided by 5.

So for any integer group Z, we can have infinite number of subgroups Z, 2Z, 3Z, zooming in 5Z, it is a subgroup, and there are 4 more cosets: 1+5Z, 2+5Z, 3+5Z and 4+5Z.

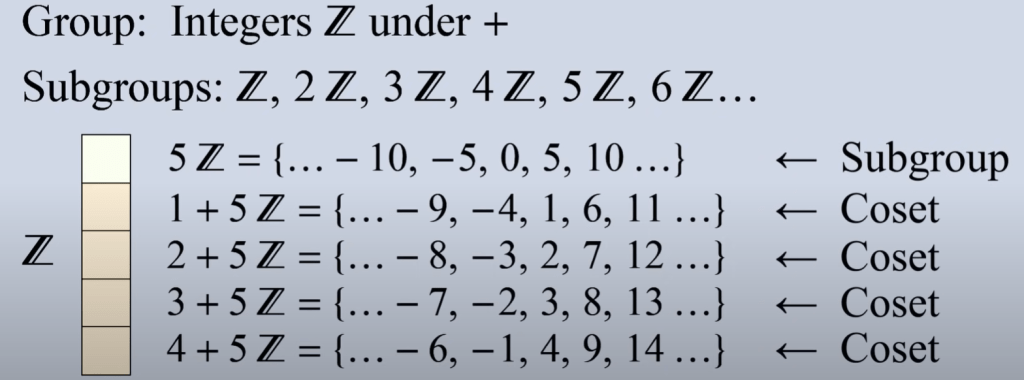
We call group of cosets a “Quotient Group” even they are not strictly “Group”. They are expressed like below, so you can see where “quotient” is from. Cosets can be added.

Next, an important question to ask is if cosets can form a group?

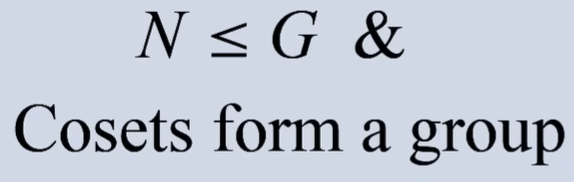
then we deduce

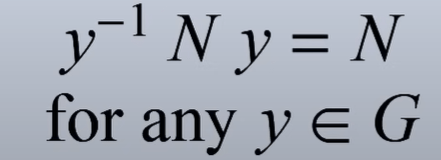
Conversely it also holds, that means if conjugate of any element in G to N is N, then cosets form a group.

To summarize and coin the terms:

If the normal subgroups for group G only contains a trivial group {1} and the entire group G, then we say this G is a simple group.

Let G be a finite group, if we can find N1 as the maximum and proper subgroup for G, then subsequently find N2 as the maximum and proper subgroup for N1, until reaches the trivial group {1}, then we got composition series, also called a normal series. It’s similar to the prime factorization to integer group.

There are 4 stes of finite simple groups:
1) Z/pZ, where p is prime.

2) polynomial equations. There is a famous conclusion in mathematics that there is no general formula for solving equations of degree 5 or higher.

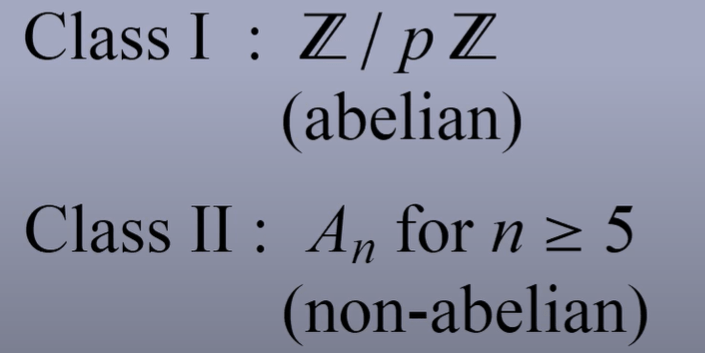
3) Groups of Lie Type (Lie Group). This is a group deals with Manifold. Note Manifold is a space which looks like R^n up close but very different very take microlevel view. for example, complex number Z that have |Z|=1 forms a Lie group, it’s a ring with radius of 1 but when you go closes, the arc can be viewed as a straight line – Einstein’s general relativity relies heavily on this math theory.

Within this Lie Group, there is Matrix Lie Group, the definition is as following:

From Keena Crane’s speech on Lie Group Integrator on Vehicle Animation and Control,

4) 26 Sporadic Groups including the happy family /monster group contains 20 groups, and pariah group containing the rest sporadic groups.

Further intuitive explanation and motivation of normal subgroup is provided by Mathew Salomone, he points out the normal subgroup is fundamental building bricks of group, not any subgroup can be “normal subgoup”, it has to be able to guarantee that any two cosets aH and bH, should have (aH)(bH) = abH, by allowing conjugacy!

it’s easy to prove if [G:H]=2 such as alternating group/reflection, there is always a normal subgroup.

What’s the use of normal subgroup?

We can find that the normal subgroup is made up of the identity row (first row) and the 2+2 row, how and why, needs to prove it. the part of how can be via Lagrange’s theorem, the the cosets order divided order of G. hence there is no other combination except first and third group, the order sum is 1+3 = 4, which divided 24, the order of S4.

Then we can look at groups with the perspective of “factor group”, what is factor group? the factor group, denoted as G/N like Z/4Z has 6 element cosets, or elements. every one inside the element behave blindly same.

Since each element inside the coset is blindly interchangable, hence N is “blindly” same or collapsed to identity, and factor group (), (12), (13), (14), (123) (132) is same as (), (12), (13), (23), (123) (132), the S3.

Another example

Lagranges theorem is correct only in one way, conversely, not necessary. Cauchy’s theorem added the constraint of abelian and prime conditions and make the other direction also valid:

What’s so powerful in short exact sequence

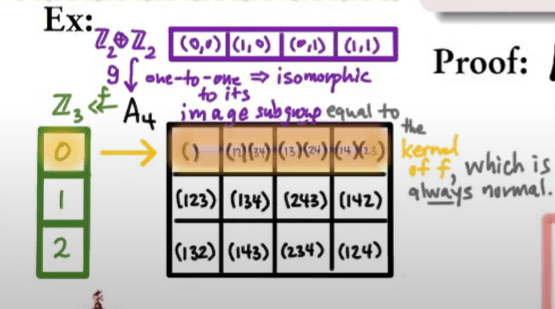
Here is an application to study groups of prime-square order, or classication theorem