What is a Cyclic Group. The definition is

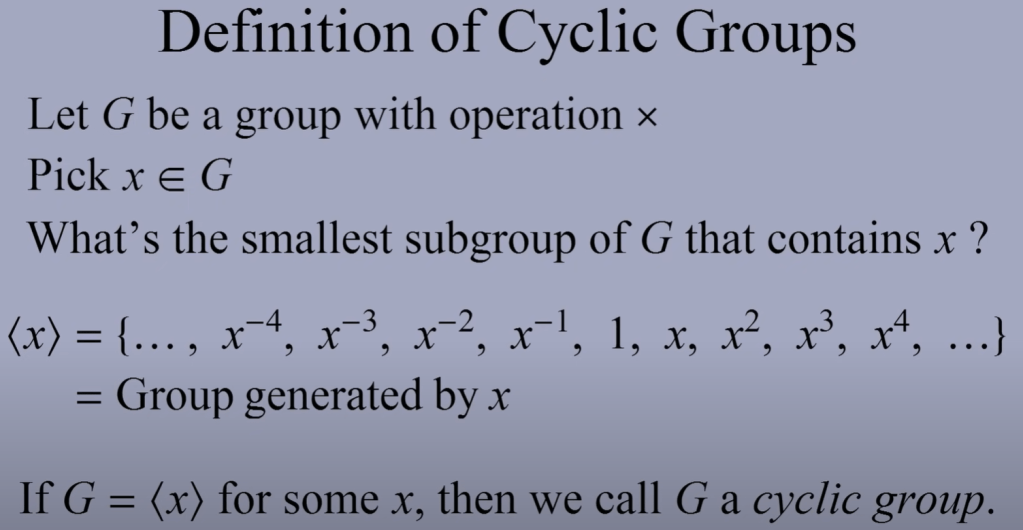
A concrete example of cyclic group is integer group as it can be generated by 1. Let G be a group with operation +, pick any element belong to G, <1> can be generated by identifying the identity 0, add one, add one more…

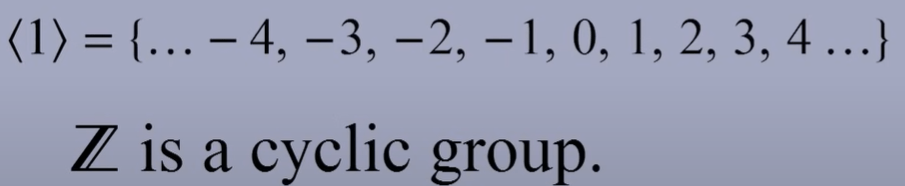
Cyclic group can be infinitive as above, also it can be finite:

Actually there are only these two cyclic groups:

Next big topic, how do mathematician compare two groups, measure up how similar they are. They use homomorphism. First, compare these two groups see how strikingly similar they are to each other:

Now to figure out a function that maps between two groups.

(Z/4Z, +) and group of {1, -1, i, -i} closed under operater x, use Carley table to compare:

We found

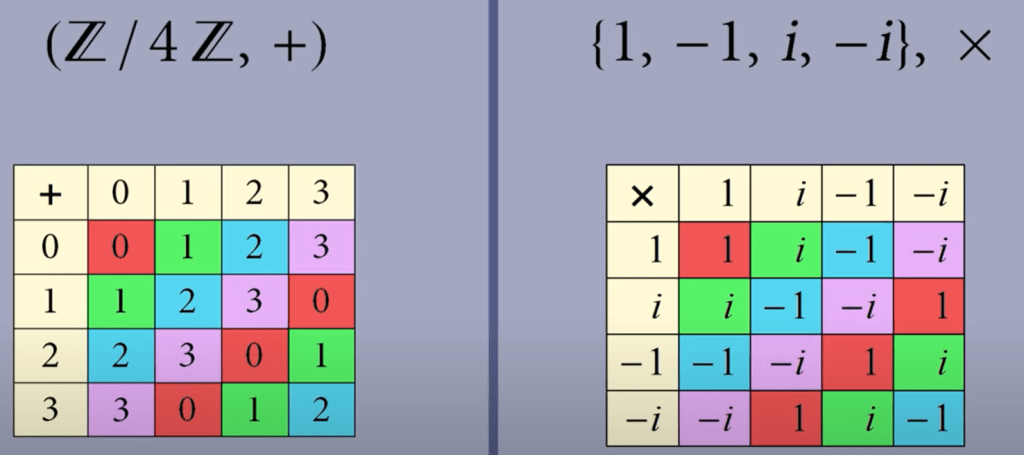
These two tables are equal form, or use the terminology – isomorphic.

When we can use a function to map between two groups and satisfy the below equation, we call it homomorphism.

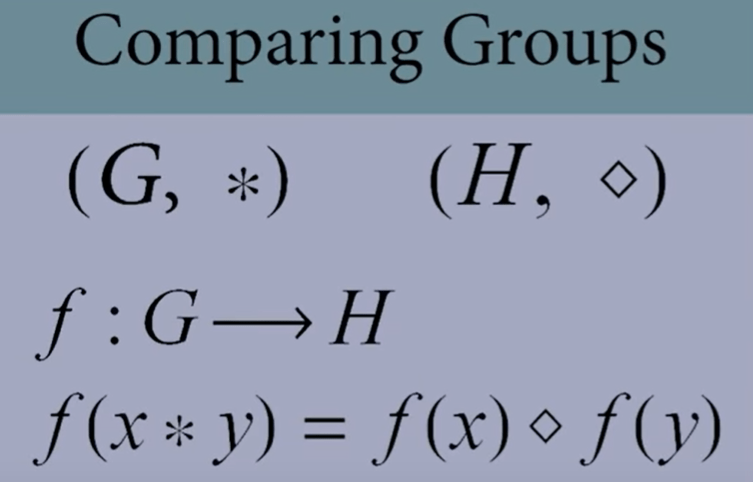
Applying this with an example, integer group to integer group on a function f(x) = 2(x), the two are homomorphic.

Another example, to judge below two groups under that particular function is homomorphic or not. The answer is yes, because e^(x+y) = e^x + e^y

One more example,

However, in this case, we found

So homomorphism doesn’t require one on one mapping. After the word homomorphism just means same shape, not exactly same.