The notation of symmetric groups for example S3 is a group of permutations on a set with 3 elements.

Since it’s a group, what is the operator, say multiplication here? Mathematicians view it as function/mapping between elements:

The size of S3 = 3!, is called the order of the set. Note there is another notion “order of element” also use absolute sign but means very different thing.

Notation is very important, here is a significant time saving notation for denoting the function and function composition:

when we switch order the result is different so it’s not abeline or not commutative. Symmetric Group is very important and has profound application for example computer science, there is computational algebra.

Another brilliant example of how important NOTATION is is cycle notation to denote permutations. How this is performed is easier to reference this link. Note two permutations with common numbers are not commutative:

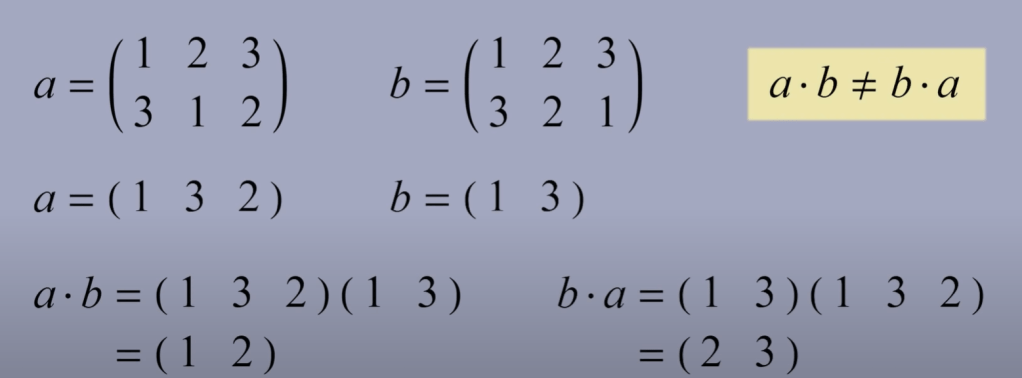
Geometry there are dihedral group that is also symmetric group.

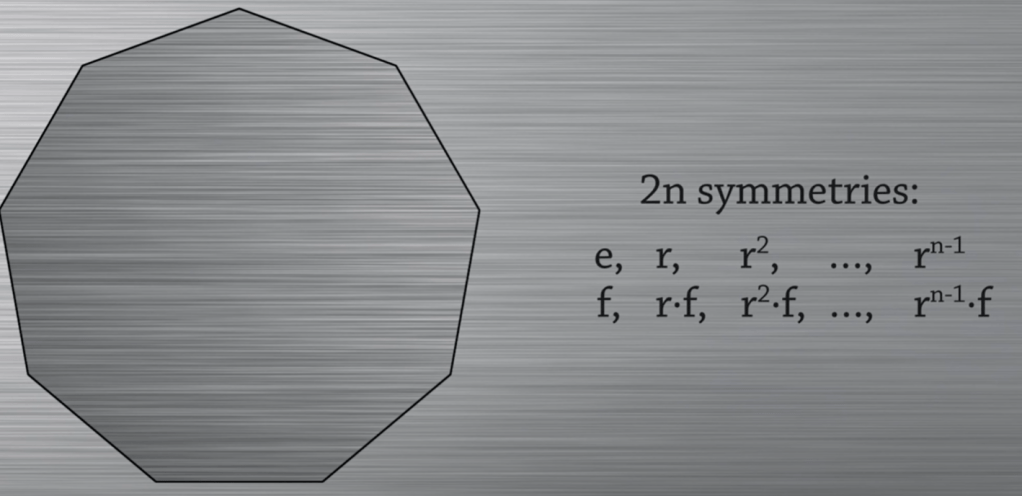
because r * f <> f * r the dihedral group is not commutative.

It’s fun to study symmetries of equal triangle – Symmetry Groups of Triangles