Mathematically, Ring is defined as a set of elements that can add, subtract and multiply under closure but you may not have division. For example, all integers are a ring, you can add, subtract or multiply but if you divide two integers, the result may not be an integer again. Another example of Ring is Z[x], polynomials with integer coefficients. Officially

To generalize, Ring is just a particular form of Group, where not only one single operator, either add or multiply is allowed but both. However down to the below 4 types of Groups, arithmetic rules work or not work in various manner:

Here is a more official or sophisticated definition of RING

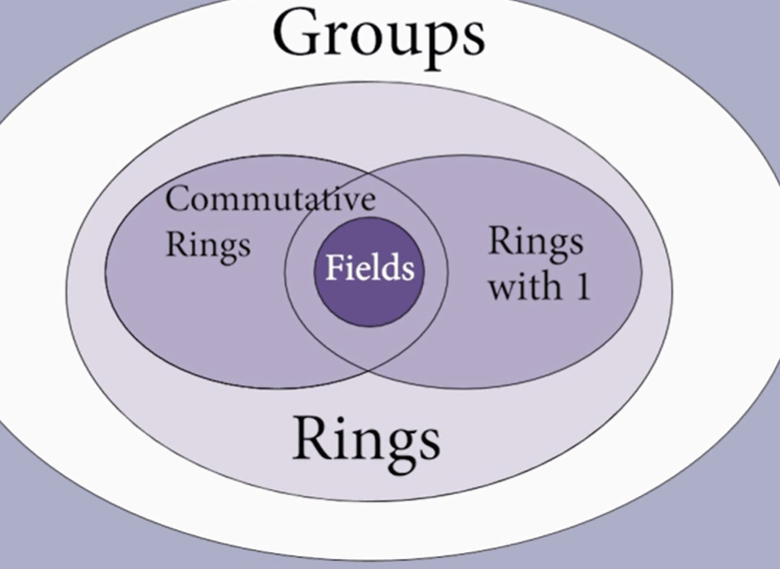
There are different types of Rings. commutative ring, division ring (that has inverse for multiplication). These two doesn’t have to be consistent. There is a Non-commutative division ring, called Quaternions (sort of complex numbers not limited by one imaginary number i, but j, k etc.). Finallly the highlight, the Commutative Division Ring, we call it FIELD.

There are examples of Rings to help understand. One interesting example is the “even integer ring”. It doesn’t have identity 1 under multiplication, because 1 is odd.

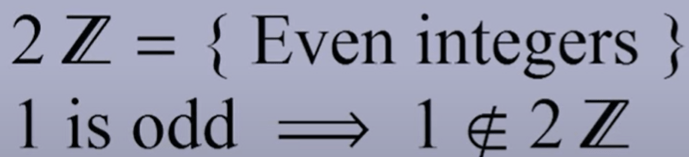
We know matrix ring is not commutative, but it could have identity. However, if we define even matrix ring as below, it is not commutative nor does it have identity.

Above rings all seems to be infinite, are they finite rings? the answer is yes. for example, quotient group, or here more precisely should be called quotient ring, Z/nZ, they are finite, commutative and has identity 1. n can be any number, if it is a prime, then this ring is called Field. Every field is a ring but not every ring is a field.

another illustration is

About Ring, there is the concept of “units of ring”, defined as the unit in Ring that has an inverse also in ring, for example

Another example is the integer module 12 has 4 units 1, 5, 7, and 11.

Let R be any ring, then units R^x are a group.

Why we define units. to introduce another concept called Associates. multiply units of a ring with integers, for example in the first example here the “integer Z”‘s unit Z* is {1,-1}, multiply it with 2 we get Associate {2, -2}. It further leads to the Fundamental Theorem of Arithmetic: Every integer n has a prime factorization that is unique up to order and associates. (n<>0, +-1).

Most matrices in R do not have multiplicative inverse but the below one is an exception: