What is Field, Loosely speaking, a Field is a set of elements that can add subtract, multiply and divide, and they are commutative.

Other than sporadically mentioned in previous blogs, the official definition is as following

The below two fields are rational group and the integer mod prime. Also there is an extension 2, 3, 5 … called characteristics. For Rational Group Q, the characteristic is 0.

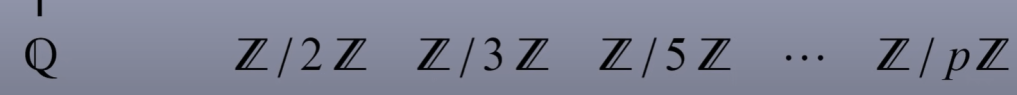
Famous fields are rational number, real number and complex numbers.

However, square root of 2 is not a rational number, is there a way to include such elements and form a field? Yes, just throwing square root of 2 into Rational Number group, this is an extension group/field

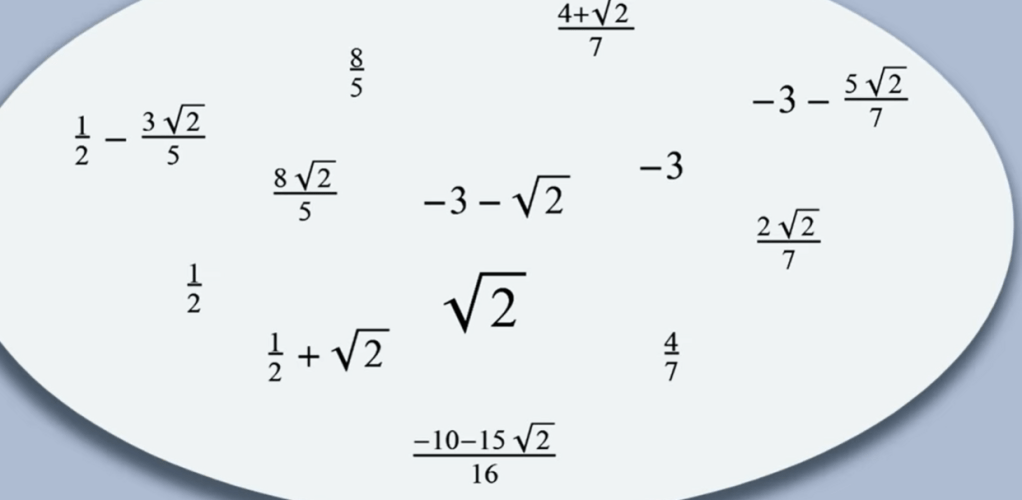
This mindset can be extended to infinite more, one of them is calculus.

But actually real number field is still not “complete”, we need to add the imaginary number i into it, and form Complex number field C = R(i). And C is “really complete”. We say the complex numbers are “algebraically closed”.

Exciting part, abstract from the limitation of physics, from pure abstract algebra perspective, we can liberate constraints and define vector space as

based on this definition, we know matrices are vectors, real polynomials of degree 5 or less, or the below vectors – function that is continuous on R. This is the moment you realize we don’t have to always understand vectors as arrows with tail and head. It’s generalized!

Vector space can be further generalized, that is MODULE.

If the scalars are Ring, it’s module:

To compare the two, or deeply understand module, let’s take a concrete example, note below the scalar ring is a matrix.

Modules are more complex than vector space.