This professor Keenan Crane from Carnegie Mellon University is amazing. I was happily surprised to watch his course on Computer Graphics (CMU 15-462/662) However, to really get a hang on it, I decided to take his course on Discrete Differential Geometry(DDG) first.

The road map is as follows:

In the very first two lectures, he reviewed the basic concepts in vector calculus and linear algebra. To refresh, here are the important ones I cited out for myself: Tangent and Normal:

Curvature describes how much a curve bends, quantitatively or more formally, the curvature of an arc-length parameterized plane curve can be expressed as the rate of Tangent change.

Why don’t we just take the norm(magnitude) but the inner product of normal to tangent change (or second derivative of arc s change), the answer is to keep the sign.

Now back to DDG, the curve is not smooth anymore, how to measure “curvature” is a practical problem:

So mathematicians are clever to come up various ways to measure curvature in DDG: turning angles, variation of length(gradient), Steiner Formula and Osculating circle.

AS to the last one, osculating circle, it’s the familiar formula – it equals to the inverse of the radius.

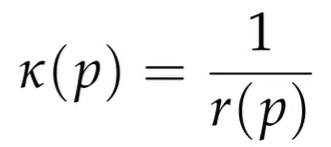
in DDG, then

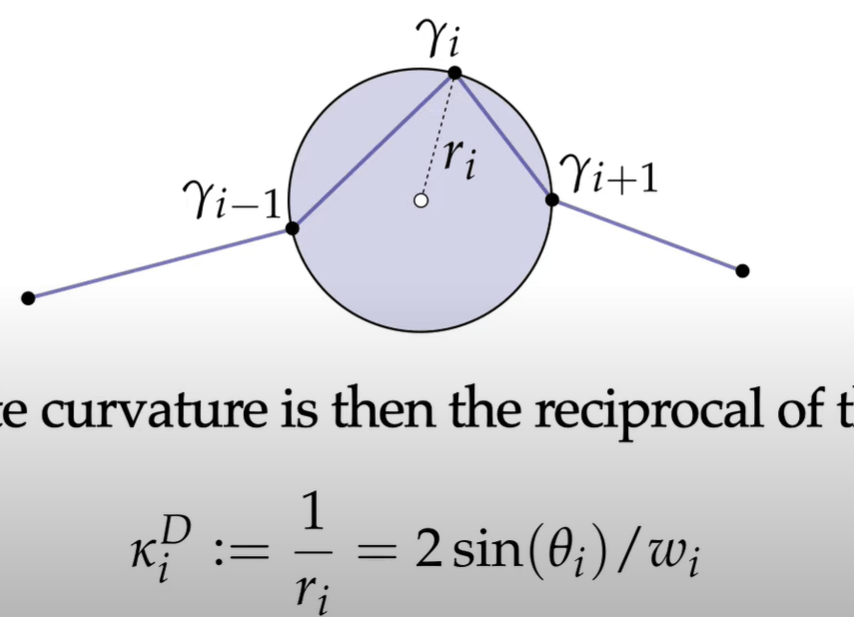
In real life, picking which approach to measure curvature depends on concrete problem at hand. Nothing is perfect.