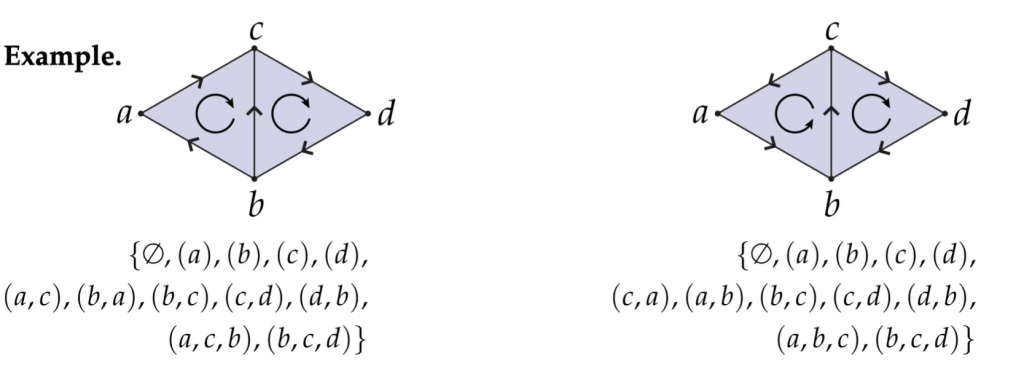First, let’s understand the concept of convex set and convex hull.

Then the concept of simplex: A k-simplex is the convex hull of k+1 affinely-independent points, which we call its vertices.

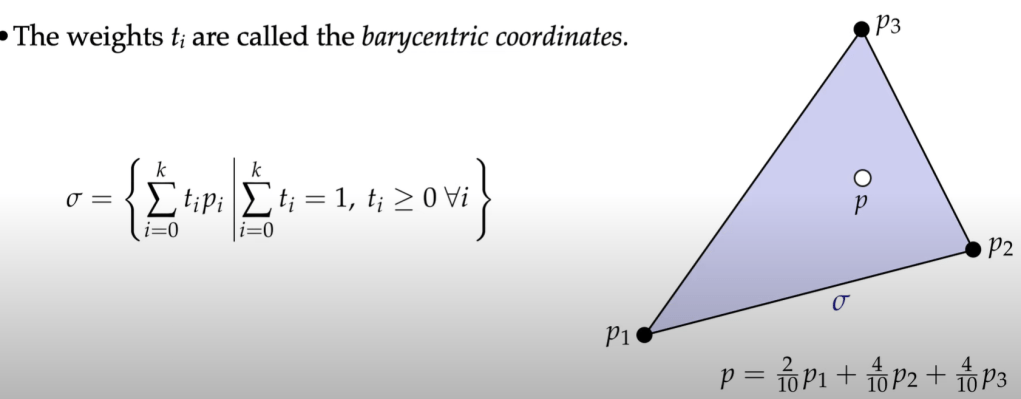
Barycentric coordinates: the nonnegative weights t is the barycentric coordinates.

Put all these simplices together we get simplicial complex or mesh. The geometric definition of simplicial complex is a collection of simplices where the intersection of any two simplices is a simplex, and every face of every simplex in the complex is also in the complex.

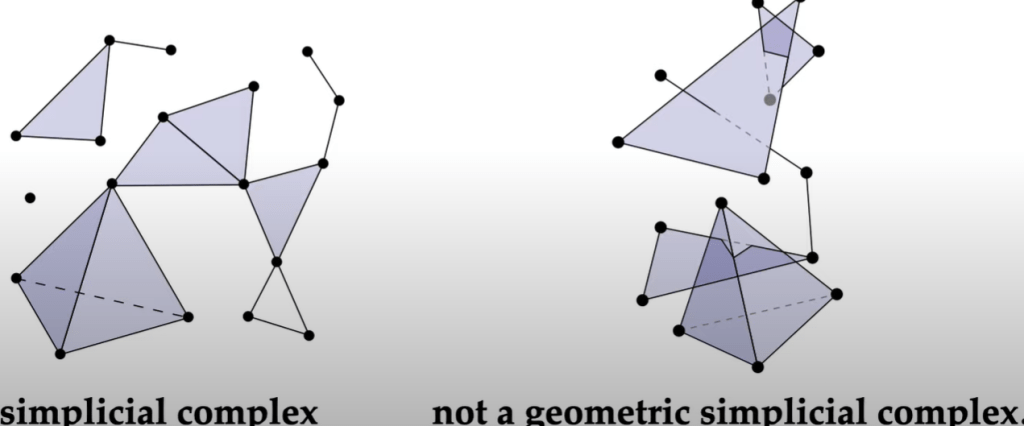
the latter one’s geometrical arrangement makes it fails to be the simplicial complex, but it is an abstract simplicial complex.

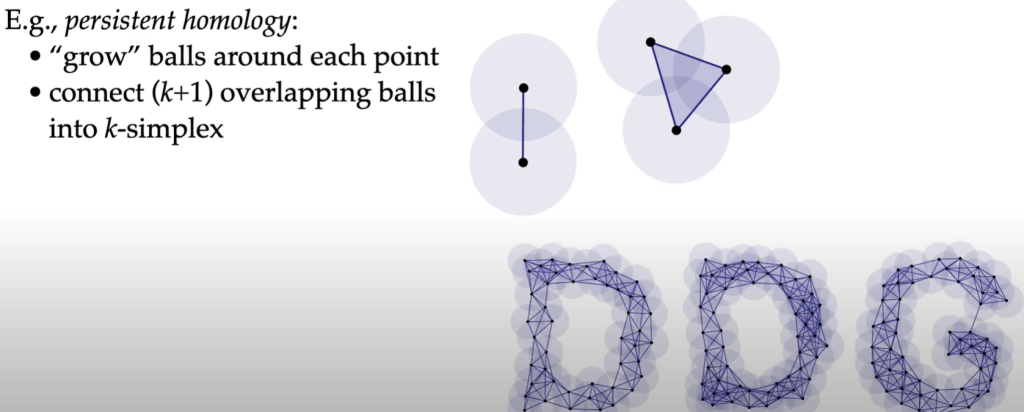
To understand data via connectivity is developed into topological data analysis, which has profound application for example to grow dots and recognize dots like below:

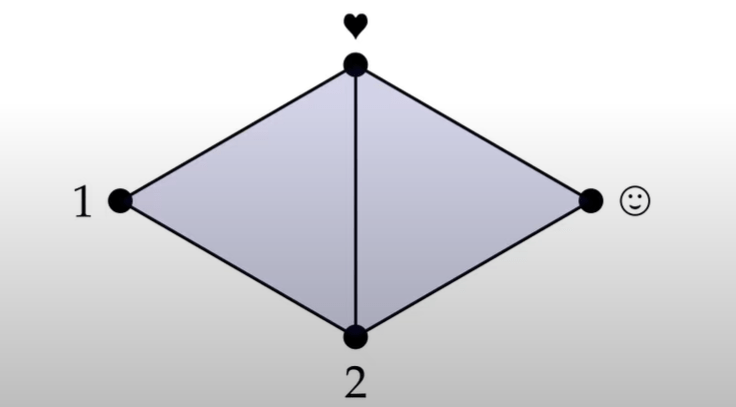
Anatomy of a simplicial complex, there is closure, star and link. Closure means the smallest simplicial complex containing a given set of simplices. Star is the union of simplices containing a given subset of simplices. Link is closure of the star minus the star of the closure.

for simplicial 1-complexes(Graphs) we write G =(V, E), for 2-complexes(Triangle meshes, we write K = (V, E, F). V means vertices, E means Edges, and F means Faces.

An oriented k-simplex is an ordered tuple, up to even permutation.