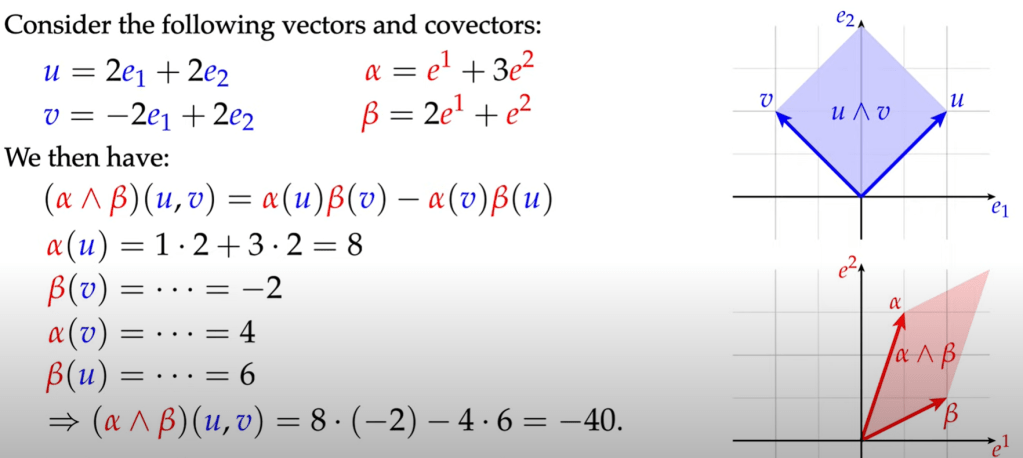In DDG, to learn Exterior Algebra is a must to build up skills and knowledge to compute meshes.

First, we need to know the concept of inner product and wedge product. It’s a signed quantity generated from u wedge v. The output is also called k-vectors. So the below u wedge v is a 2-vector. 0-vetor while is just a scalar.

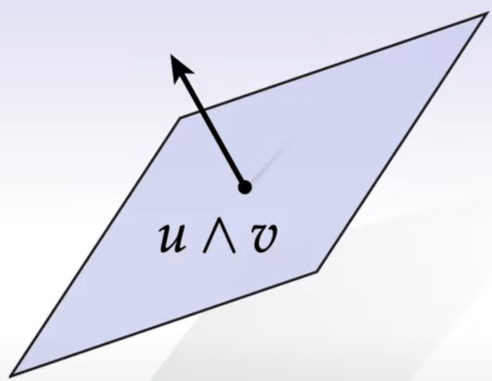
Orthogonal Complement, geometrically we are very familiar to denoted as the V vertical line,

written down in rigorous math language it is

Knowing Orthogonal Complement, you can easily understand Hodge Star. It has great computational advantage to use one single w (orientation and magnitude) to express the wedge product of two vector u and v.

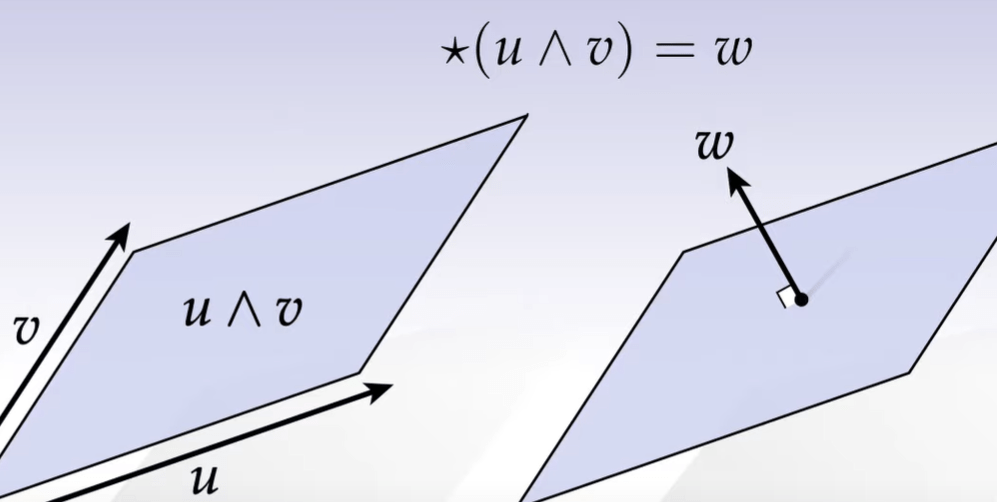
To define the sign, the convention is z /\ *z = positive. Visually it’s 90 degree counter-clockwise rotation. One caveat to be noted is that anti-intuitively, **u is not equal to u but to the opposite direction, only ****u = u in 2D.

As we know how to express a vector using the combination of independent basis vectors each scaled by a real number, the basis vectors do not have to be limited by only 1-dimension. In a R^3 space, we can have basis-2-vectors and basis-3-vectors.

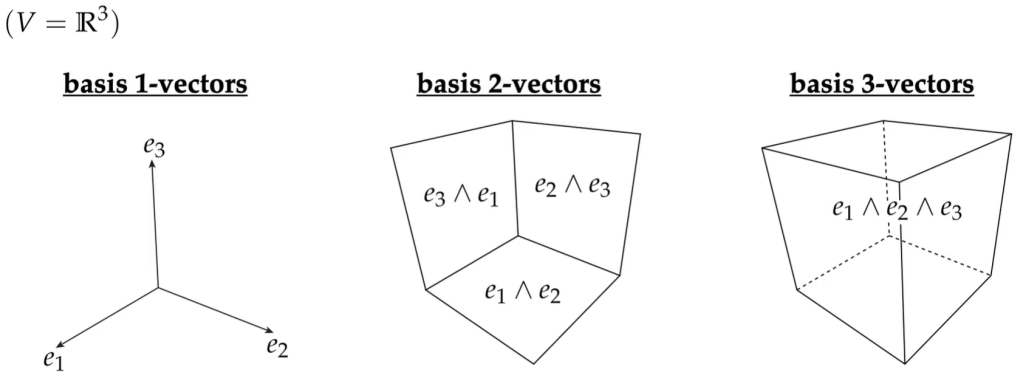
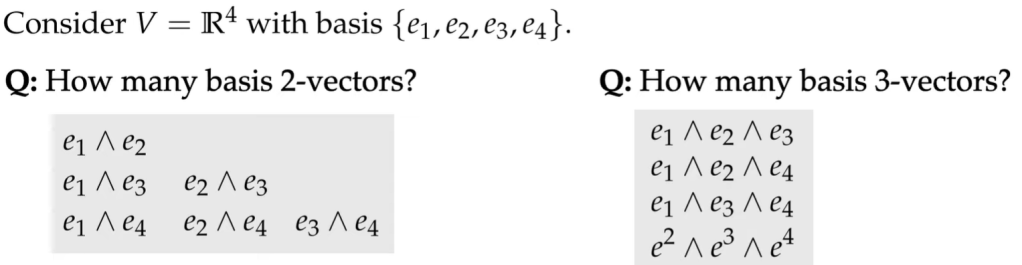
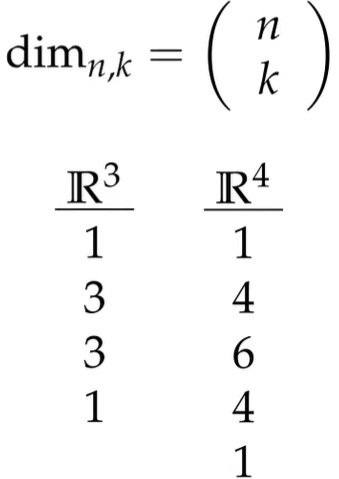
There is a pattern in figuring out how many basis-k-vectors for a space V:

Note the way mathematicians call u wedge v is a 2-vector. Now we can apply to solve the simplest computational problems. It’s to plug in the basic computational rules based above knowledge.

K-Form. To understand k-form, first we need to know vector-covector duality. it’s essential to seperate the vector to be measured and the measuring metric.

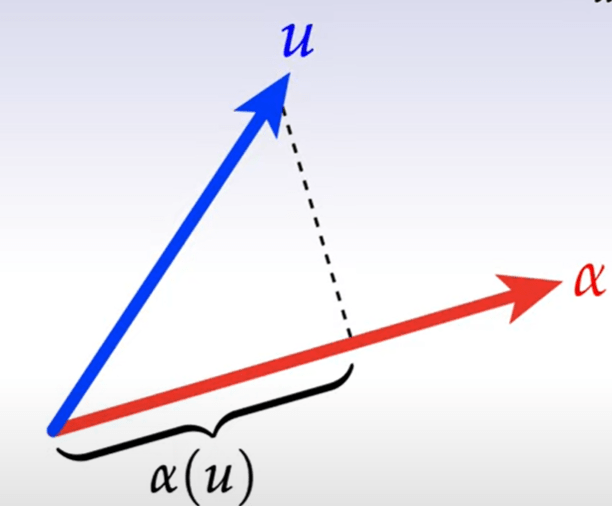
All these metric vectors formed a space called V* dual space, following the same characteristics of a vector. These metric vectors are called dual vector or co-vector. Co-vectors can be functions.

Mathematic convention, for computation of dot product of two vectors, we transpose the first one to be a row, then compute.

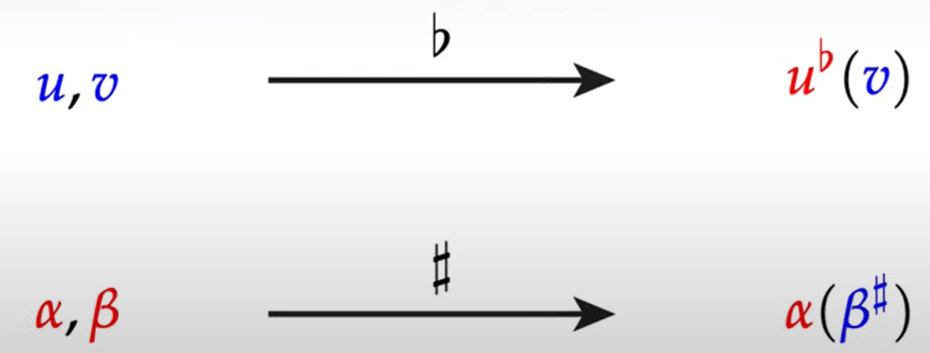
The notation/convention is particularly useful when dealing with below form

Just as covector measures vectors, we introduce k-form to measure k-vectors

the measuring follows the same logic in 1-vector that we’re familiar with, just to think of projection of 2D to 2D, rather than 1-D to 1-D.

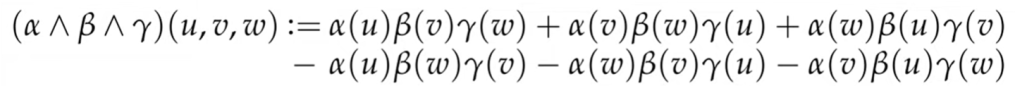
k-form is a fully antisymmetric, multilinear measurement of a k-vector, think of it as a map from k vectors to a scalar. Linear in each argument is reflected in below two examples, note this is not as familiar so need to practice the rule:

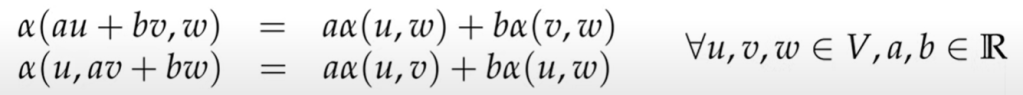
for 3-forms, we express application of k-form via determinant. it’s also consistent with the notion that it’s capturing measurements of volume.

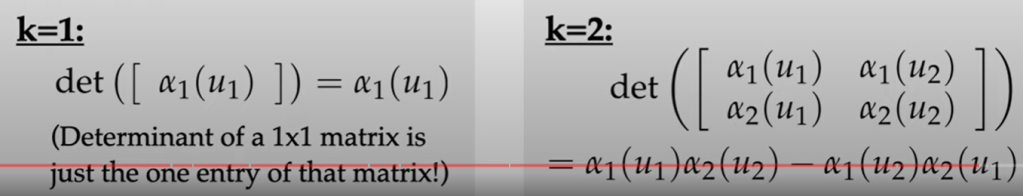
To facilitate the real computation, we need to introduce coordinates in vector, covector, first, what we are familiar with is the vector space

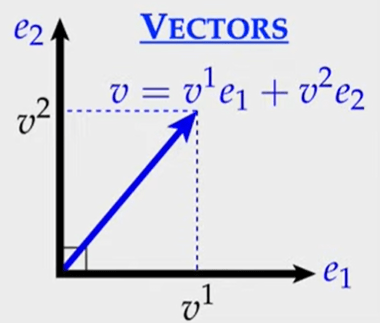
what we are not familiar with but need to be trained to get more familiar is the co-vector space

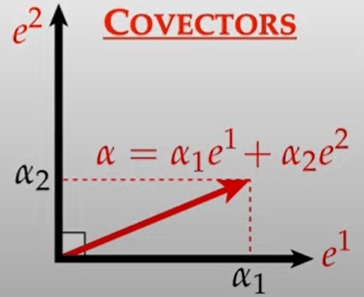
To have the feel how these seemingly esoteric vector, covector math systems help solve real problems in a grand scale, let’s illustrate with a 2-form example.