The whole purpose of learning Exterior calculus rather than simple vector calculus is to handle volume(higher dimensional) change computation. The wedge, k-form, differential k-form concepts greatly help solve this difficult problem in math and physics.

Review of derivative, divergence and curl

Correspondingly, we have the following for exterior derivative. Be sure to note that d(differential) is a unique linear map that project from k space to (k+1) space:

The directional derivative of a scalar function phi at a point p with respect to a vector X is the rate at which that function increases as we walk away from p with velocity X. In describing it try to get rid of coordinate framework, as follows

The key concept, which is very puzzling is the concepts of gradient and differential. One is vector field, the other is differential 1-form.

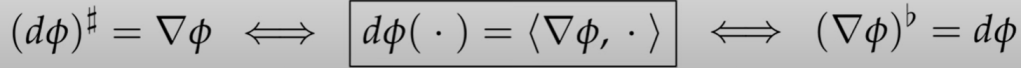
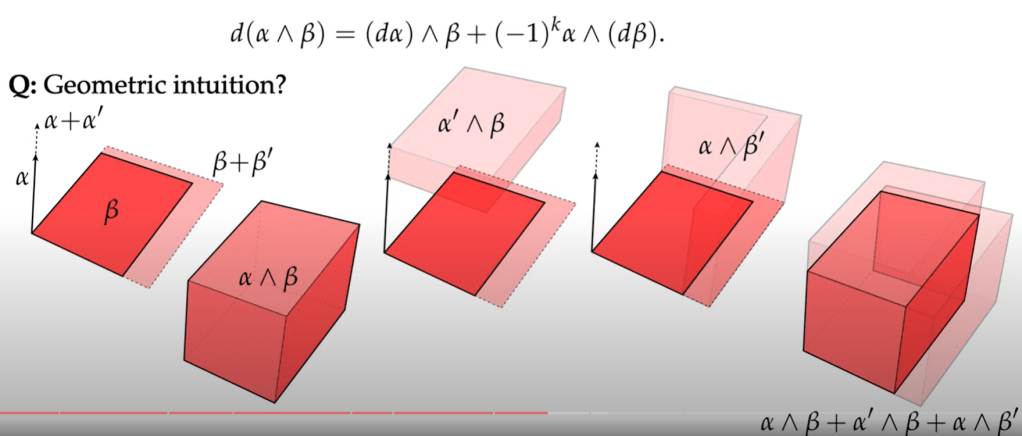
Secondly, let’s take a deep look at exterior calculus’ product rule:

The question you would ask is why there is such a product rule. It comes naturally if go to the core of “differential”:

To perform these computation, remember the base case is “0-form” or a scalar function(A scalar valued function is a function that takes one or more values but returns a single value. f(x,y,z) = x²+2yz⁵ is an example of a scalar valued function). Using the following example to illustrate:

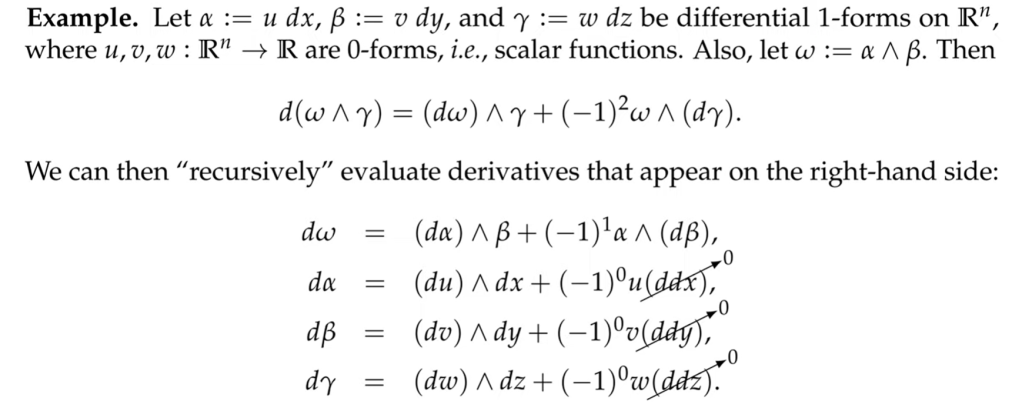
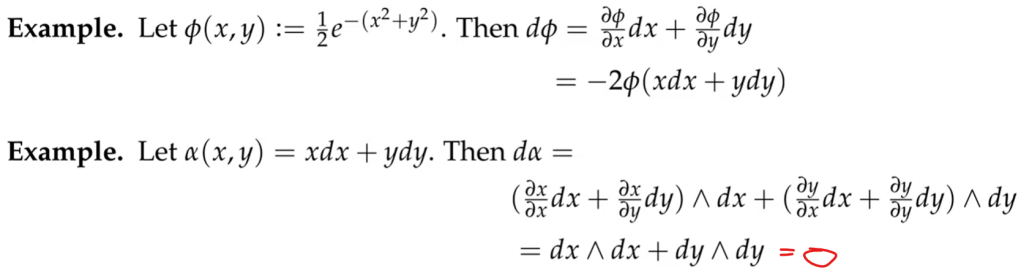
What’s worth further mulling is to look at the similarity below

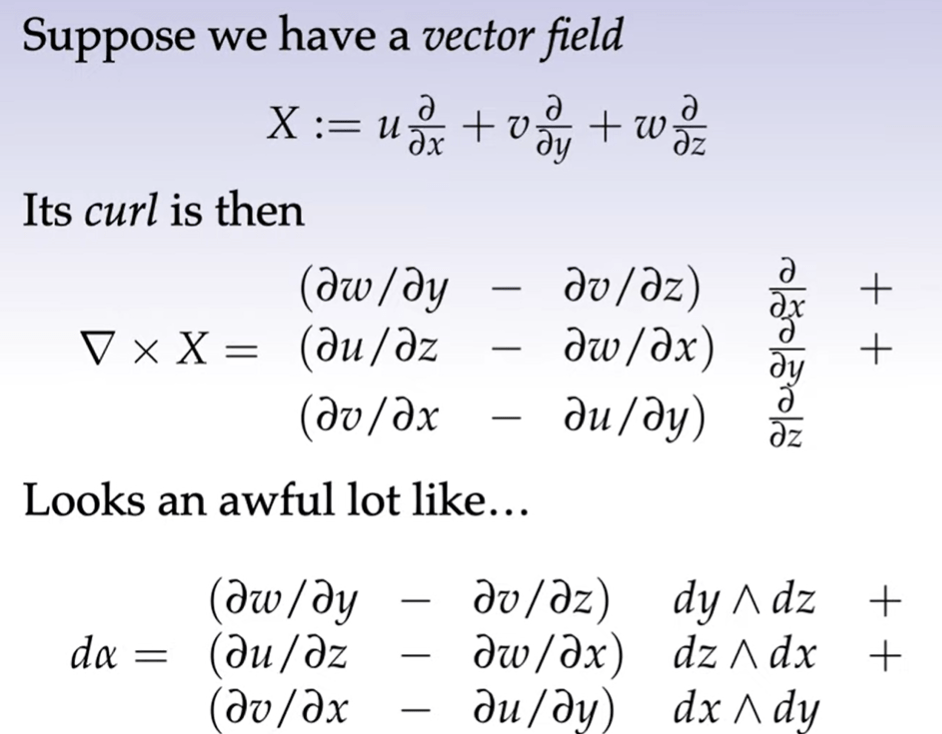
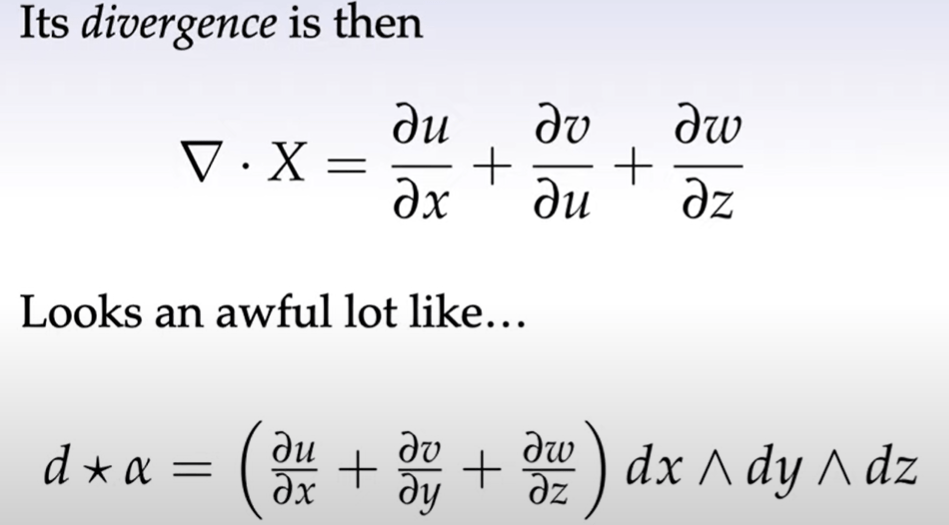
All these unfamiliar concepts makes the head spinning, as to the end, just need to grasp at least the below