In real world, lots of the PDE problems can not be solved analytically, so thanks to the modern computer computation power, numerically solving PDEs becomes the major solution. For example to solve below equation, we can apply “finite difference method”.

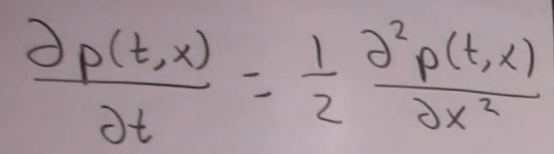
There is forward, backward and central difference. Boundary conditions are bit tricky but we can brute force define or use an average value.

Correspondingly, to solve ODEs in his playlist, “State Space Representation of Differential Equations” and “Numerically Linearizing a Dynamic System” is also detailed by him. First, what is “state space representation”? “In control engineering, a state-space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations or difference equations”. What catches my eyes is the matrix form of the state equation, debunking all the power of matrix form in math.

note: x(t) vector denotes the status of measurement, u(t) vector is the input and y(t) vector is the output.

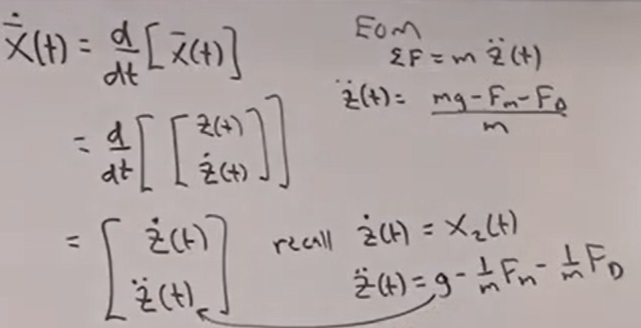
Another example on linear system

Numerical solution to PDEs is just to introduce multiple dimensions/Jacobean matrix

this is reflected in Euler Angle computation in this video.