It’s a polished version of PageRank score in our relationship data analysis.

In network problems a significant metric to characterize the importance of a network vertex is “Centrality”. There are various types of “Centrality” measurement :

Degree Centrality: number of connection realized upon the total potential connections;
Betweenness Centrality: quantifies the number of times a node acts as a bridge along the shortest path between two other nodes.
Closeness Centrality: calculated as the average of the shortest path length from the node to every other node in the network;
Eigenvector Centrality: the most complicated and elegant way; first come up with the matrix A composed of n(n is the number of nodes) column and n rows, if the two are connected, populate the cell as 1, otherwise 0. So each one’s centrality s the linear combination of your neighbor’s centrality. The math just boils down to compute the eigenvalues of this matrix.

What we calculated is called PageRank Centrality to compensate that the eigenvector centrality accounts only “undirected” relationships. However, PageRank uses the indegree as the main measure to estimate the influence level, thus this variant of Eigenvector centrality is suitable for company’s relationship analysis.

Per the inventor Page Larry, “PageRank works by counting the number and quality of links to a page to determine a rough estimate of how important the website is. The underlying assumption is that more important websites are likely to receive more links from other websites”.

A page that is linked to by many pages with high PageRank receives a high rank itself. algorithm outputs a probability distribution used to represent the likelihood that a person randomly clicking on links will arrive at any particular page. (note pages are the nodes, and links are edges)

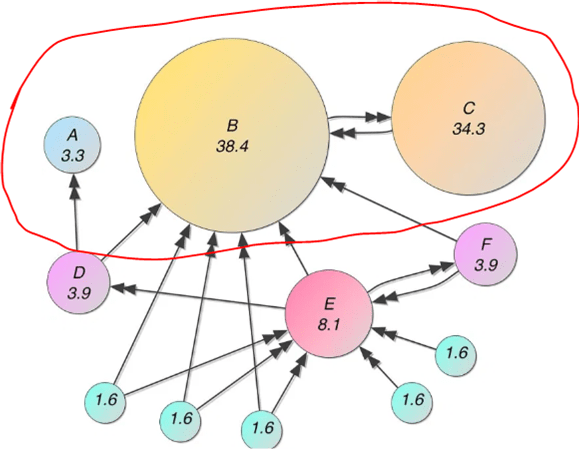
For example (from wiki), different nodes has different links pointing to them. However, not only the number of links matter, but also the significance of the node from that link, hence, Node C’s rank is higher than node E. Relationship data contains a somewhat OK scoring measurement but I didn’t include in this rough test.

The math behind pagerank is as graphed below, assuming there are A, B, C, D four nodes pointing each other.

Using a simple example, in the below matrix of 5 x 5 States matrix,

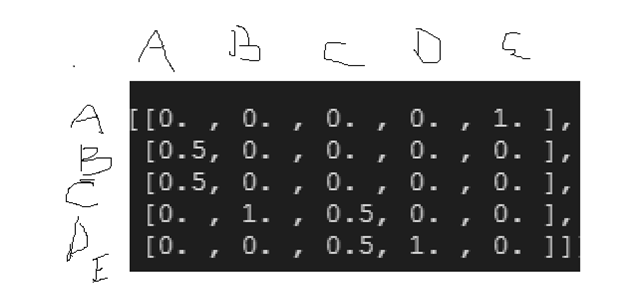
state A is pointed by state E only, while state C is pointed by both B and C, state E is also pointed by two states only, but the two states themselves (state C and D) have higher pageranke values already. Hence the output is

Similarly our relationships matrix will further transformed into a huge matrix and the open source package igraph calculated above probability.  Given the vast universe, the highest pagerank value in the previous out put is very small.

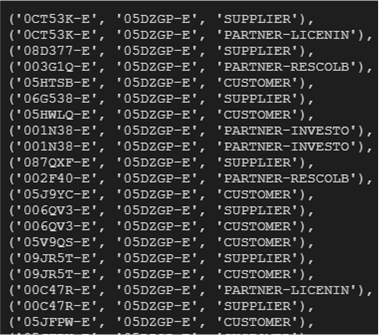
The generic eigenvector centrality doesn’t normalize hence if there are many small suppliers to a major customer such as Apple, all these suppliers are assigned a high score, which is not justifiable. The improved version-PageRank centrality overcome this issue.

In both cases, being pointed/named a relationship is needed. However what if there are no entity name it? It named other entities. Kleinberg centrality makes it possible to utilize the other direction.