Manning’s book on Information Retrieval is classical. It’s great to learn from his lectures directly.

First, what is mind-blowing is his presentation about how to apply vector-based math approach for retrieving simple questions such as “find Shakespear’s work that contains Brutus, Caesar but not Calpurnia. To search with grep brute force is not trivial or possible to some degree. Hence have a 0/1 vector to the document-term matrix arranged as below perfectly solve the issue in a fast manner.

It’s such a clever approach that it’s hard to make intuitively fast to reason out. But it does work!

Inverted Index.

Due to the enormous size of matrix, inverted index is used for overcoming this data storage issue.

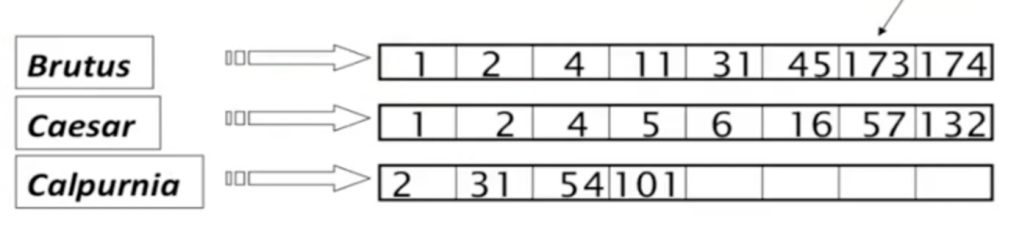
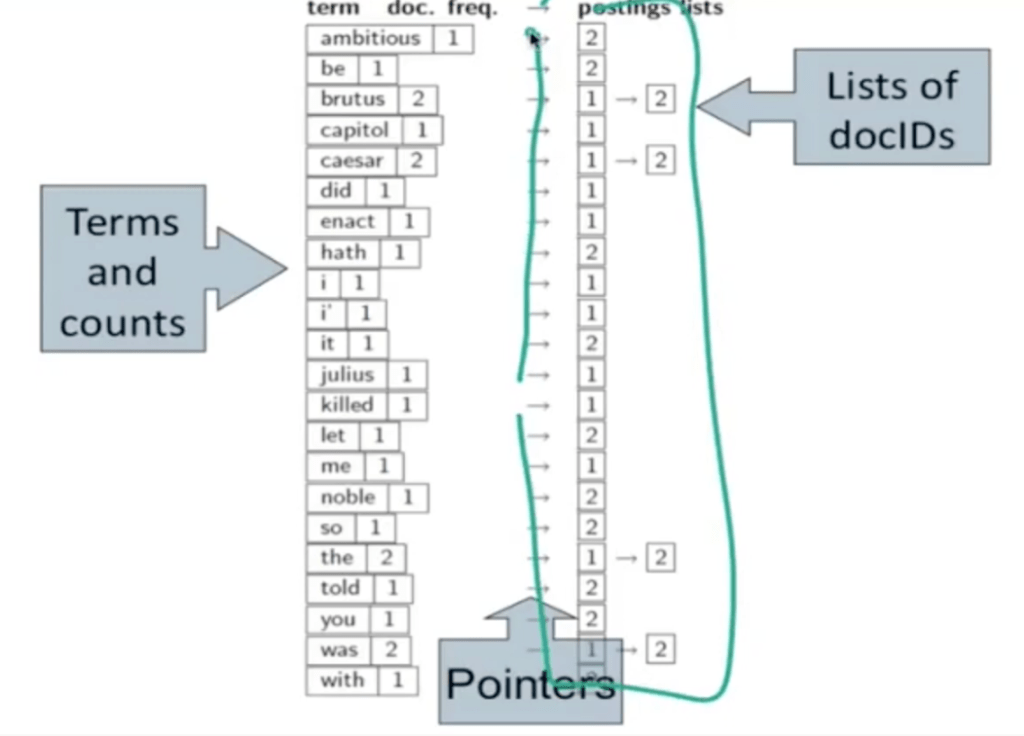
Based on this thrifty inverted index data structure, how to carry out a query such as locating document that contains both names. The mechanism is linear as outlined below

So step back to think for a search engine like Google to perform searching, it also use this “inverted index” and linear merge algorithm to do the job.

This is great but what about bi or multiple word phrases such as “San Francisco”? Here comes Positional Index.

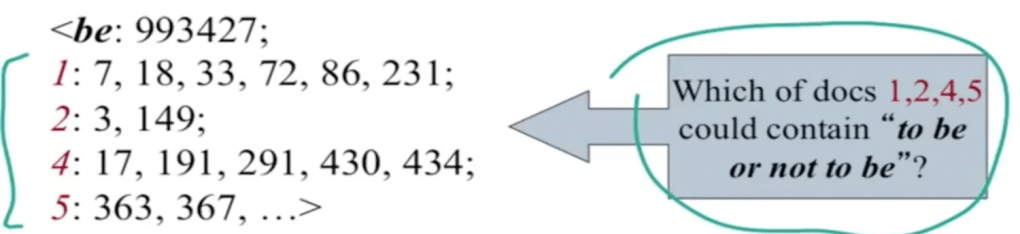
This positional index query can do what biword inverted index cannot do.

Ranked Retrieval. Above techniques are boolean queries not adequate to serve majority of real user problems which is web search. That means instead of a plain yes or no outcome producing feast or famine, an algorithm to rank the results. First, the Jaccard Coefficient scoring. A more practical scoring system is term frequency score. In term frequency scoring, instead of creating a huge 1, 0 vector for each document, only count the frequency of each word or token

This is the idea of TF-IDF model.

VSM Vector Space Model. The metric of similarity is better to be angle rather than the euclid distance.