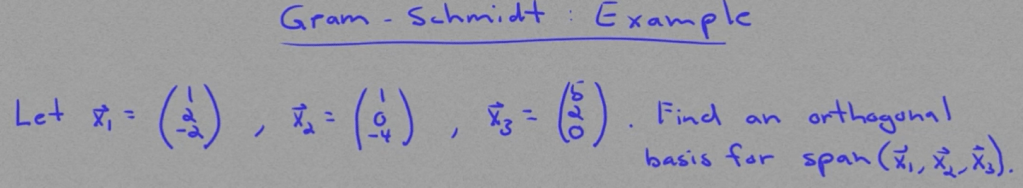Continue from last blog.
How to convert a vector (fixed) between standard basis and an arbitrary basis system?

It’s easy as follows:

just need to write it in the format – put the new basis vector into matrix, as if they are the coefficient matrix, c1 and c2 forms the real value component as that’s what you are looking for. Then per definition that arbitrary basis are linear independent, and spans the subspace, so it must be invertible. hence use P inverse and calculate the c1 and c2.
Another important concept – The Dimension Theorem | Dim(Null(A)) + Dim(Col(A)) = n | Also, Rank! Rank is the non-free, with 1 leading columns, or dimensions of the null space, while column number n – r is the free columns, which is the dimension (n-r) of column space.
Always be clear and very familiar the matrix column is converting e1 and e2 respectively from deduction above. It’s confusing if you jump to compute the matrix by multiplying row to column, totally dismissing the meaning of matrix/transformation here.
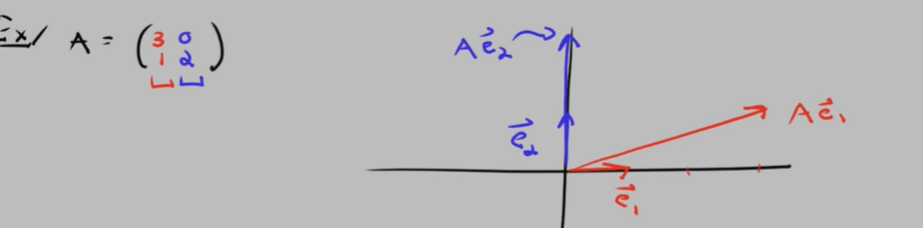
Diagonal matrix makes computation and application so much easier, we want to convert everything into it or approximate to it, That’s why there is Fourier transform. So How the Diagonalization Process Works?
For any matrix A, if we can find a series of linearly independent eigen vectors and eigen values, we can find A = PDP-1. It would be much easier when we transform/matrix. for example

To figure out how 5/4, 3/4 formed matrix work on a vector is too complicated, once we decompose it into PDP-1, it’s simply stretching on the two eigenvector(linearly independent, orthogonal axis/dimensions)! What’s more the essence here is that inverse all what P P inverse is doing is to convert between an arbitrary basis system and standard basis system. Hence if you write P-1MatrixPVector, you can think of turn the vector in its standard basis system, times P to turn into an arbitrary basis system, where transform/Matrix can be performed, then times P-1 to convert back to the standard basis system.
So in actual application, similarity and optimization is widely applied. we have calculus and now algebraic/linear algebra to tackle with. in LA sense, what is similarity? The answer is that Similarity Relationship Represents a Change of Basis! It can be proved that if the two matrices D and A worked on vector x can be expressed as below. (to be elaborated further)
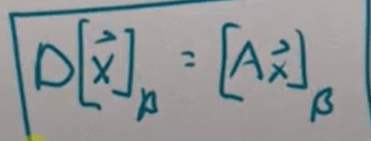
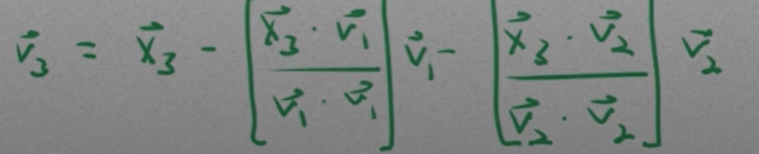
Gram-Schmidt decomposing to orthogonal basis, use a concrete example