In Bernoulli Model, what if you are not just interested in the single time estimate of the “yes” or “true” probability given the data P(theta|D), which is a Beta distribution, refer to the previous blog. Instead you are interested in knowing what is the probability of performing K times from a sample of N using the Bernoulli model? This is the Binominal Distribution. It looks like below per wiki:

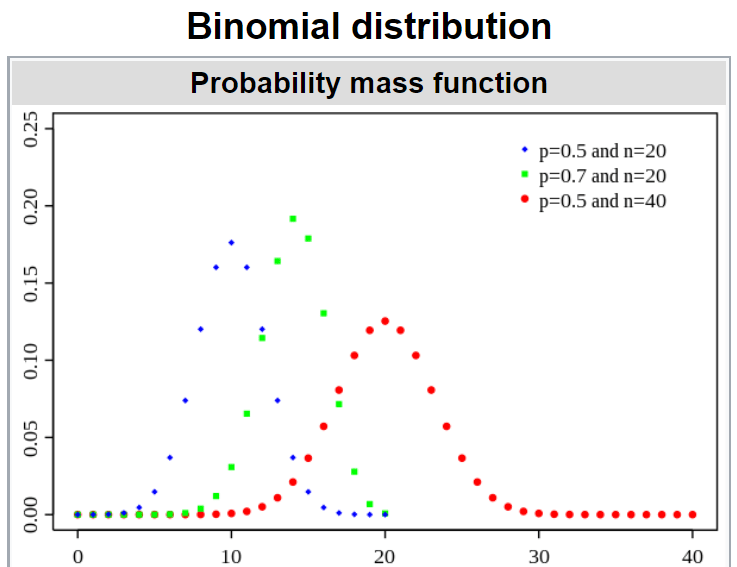
It looks like bell-shaped, however it’s not a Gaussian distribution unless the sample size goes large. The Gaussian distribution can be considered as a special case of the binomial, when the number of tries is sufficiently large. For this reason, the Gaussian distribution applies to a large number of variables, and it is referred to as the normal distribution.

What if it’s not yes/no Bernoulli model but a multi-categorical model, to compute the probability of K times out of N sample, we use Multinomial Distribution. Note it’s not the same as Multivariant Analysis.

According to this clip, take three scenario weather situation as example,

so the probability can be expressed as below:

What if the ask is for 33 days, what is the probability is 2 cloudy days, 8 rainy days and 23 sunny days?

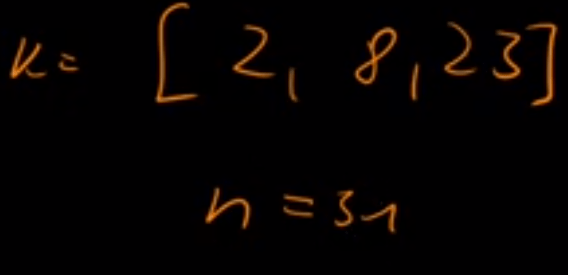
From wiki, Suppose one does an experiment of extracting n balls of k different colors from a bag, replacing the extracted balls after each draw. Balls of the same color are equivalent. Denote the variable which is the number of extracted balls of color i (i = 1, …, k) as X_i, and denote as p_i the probability that a given extraction will be in color i. The probability mass function of this multinomial distribution is:

The visual is like below