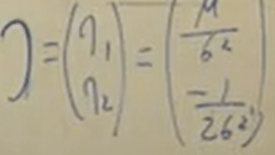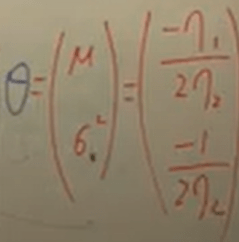Prior P(x | theta) of a Gaussian distribution can be written as following

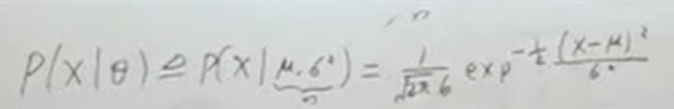
Dr. Xu rewrote in below to separate data x and parameter eta, which will make solving problems much easier.

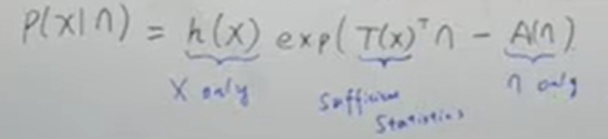
Adding here what is Sufficient Statistics, In statistics, a statistic is sufficient with respect to a statistical model and its associated unknown parameter if “no other statistic that can be calculated from the same sample provides any additional information as to the value of the parameter. for example,

What we’ve been familiar about – multinomial, binominal, categorical and Bernoulli distribution together with Gauss distribution all belong to the exponential family.

Hereunder is the conversion from Gauss distribution equation to the format

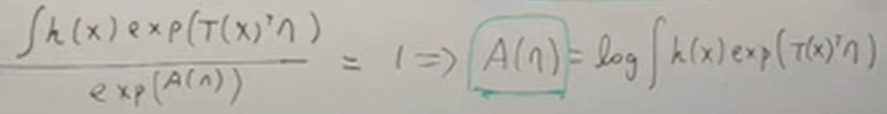
Using one-dimension Gauss distribution, let’s try to solve it without relying on the “exponential family form”,

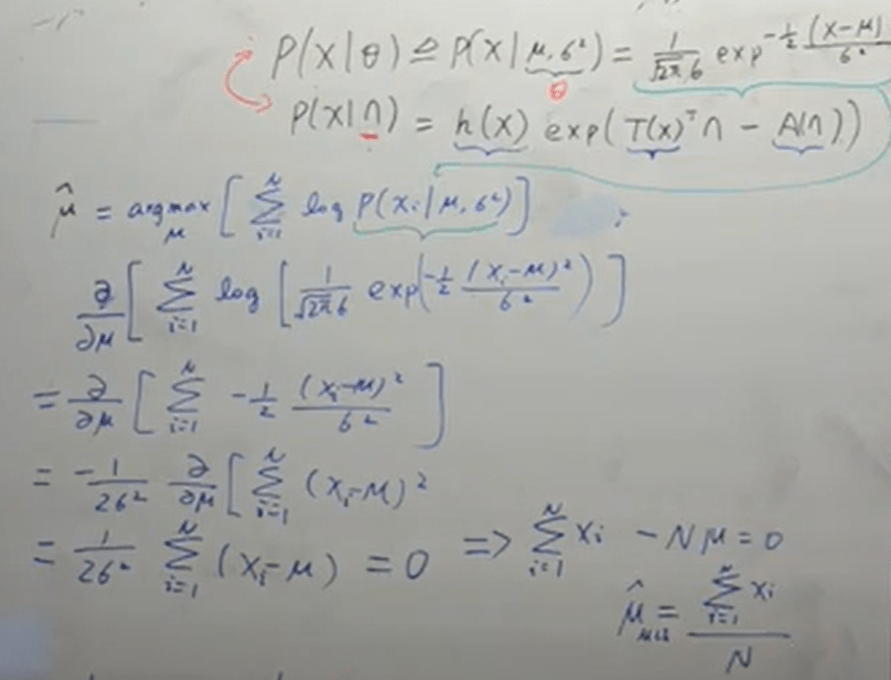
It’s deduced but with complex process. Now let’s take a look at the new approach:

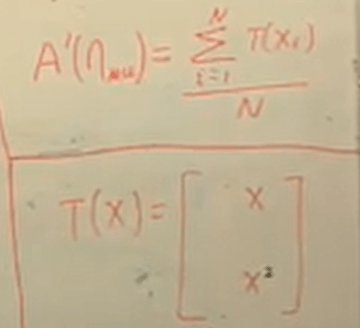
This is exactly the same as deduced step by step from original Gauss equation because