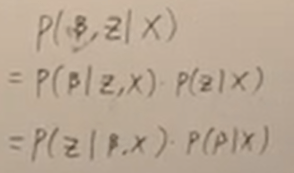If we have the prior and posterior of exponential family distribution conjugated, the computation would be tractable. So first let’s figure out the scenario when they are conjugated:

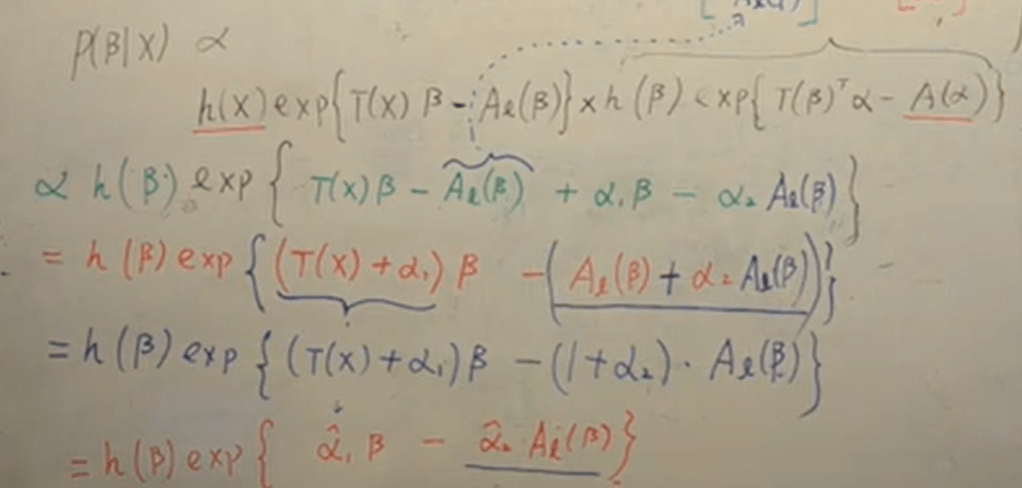
From above steps, the critical condition is “likelihood’s log normalizer is same as the second part of the prior’s sufficient statistic”, then the prior and posterior are conjugated.

Next,

first refer to Leibnitz integral

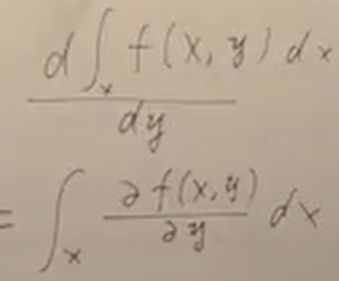
Hence we get

Next we will touch on Variational Inference. First the ELOB is the maximum of the likelihood, so we need to find a q distribution of which the likelihood equals below

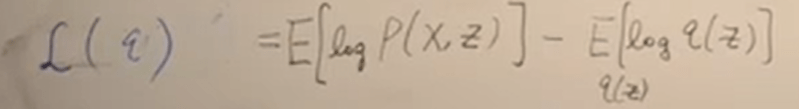
Note the joint distribution as below has the properties as: