From her homework to find relevant learning materials. The very first question is projection matrix, which is not learned about before. Wiki defines it as

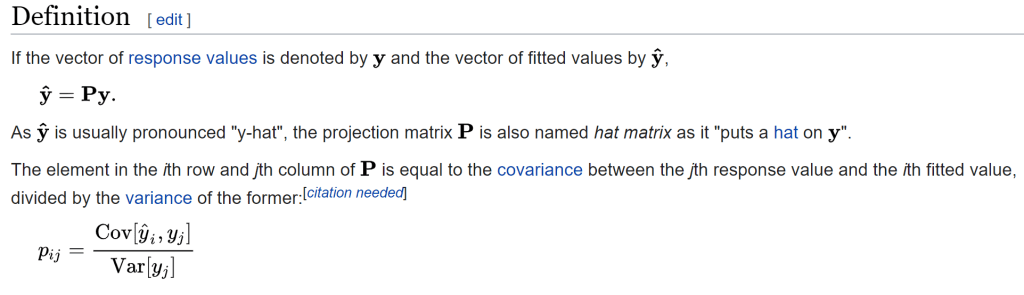
Note finding a basis for the column space of A is equivalent to finding a basis for the row space of the transpose matrix A^T. The column space of A is equivalent to the range space of A too.

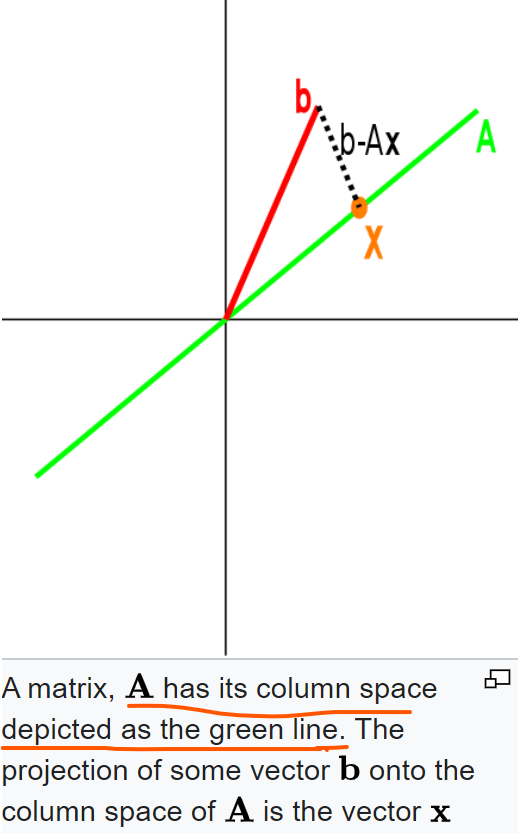
An exercise problem provided by MIT 18.06 projection onto subspace: ” Find the orthogonal projection matrix onto the plane x+y-z=0″.

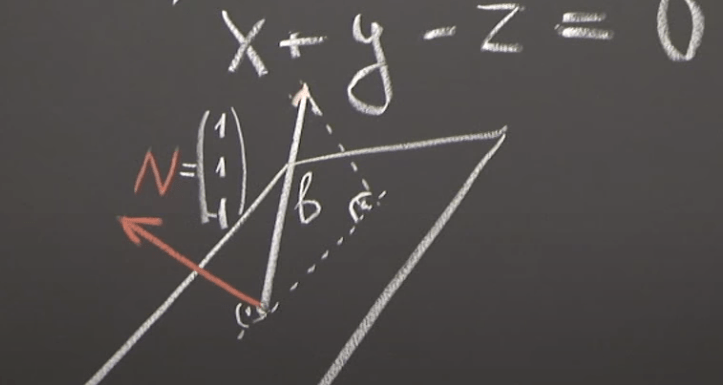
One rigid way to solve it is to apply the projection equation and pick one possible solution to the plane to form the column space/matrix A.

Another simple approach is to find any vector b is actually be dissected to pb and pNb, where pN is the basis normal to plane, so it’s (1, 1, -1).

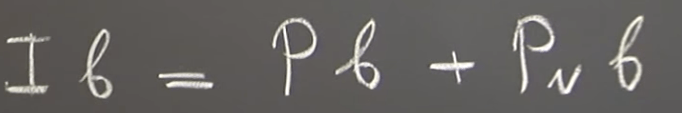
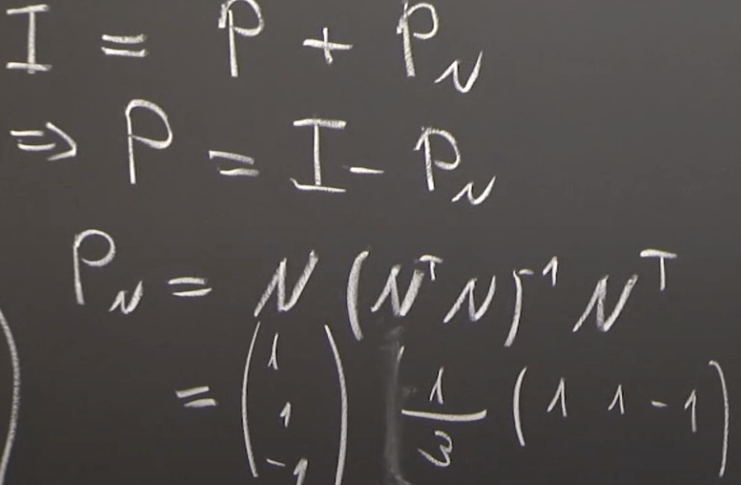
Another excise problem provided by MIT 18.06 least square approximation: “Find the quadratic equation through the origin that is a best fit for the points (1,1), (2,5), (-1,-2)”

To solve, first, come up with the equation looks like ct + dt^2 = y, then set up Matrix form

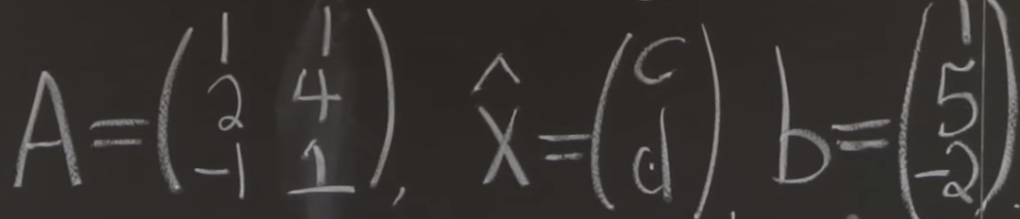
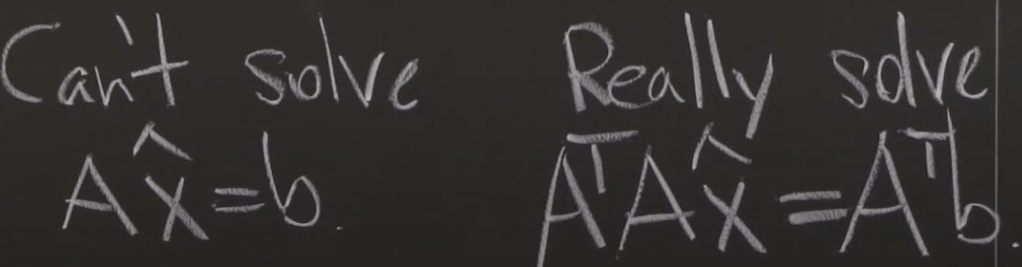
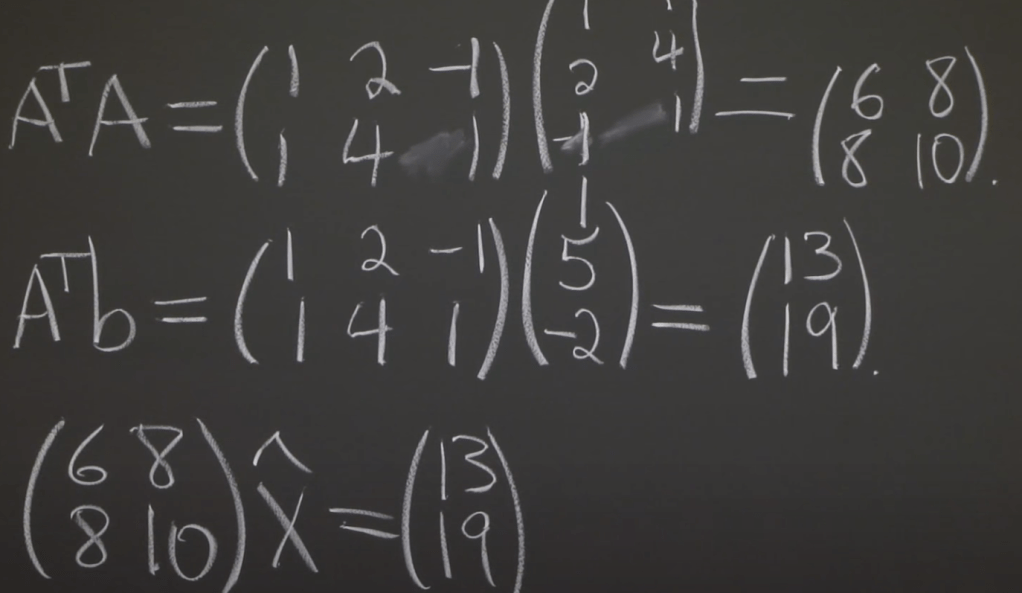
Third exercise, Solve the differential equation for the general solution. What is the matrix A?

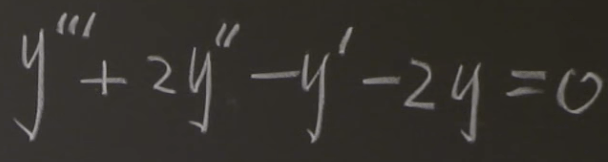
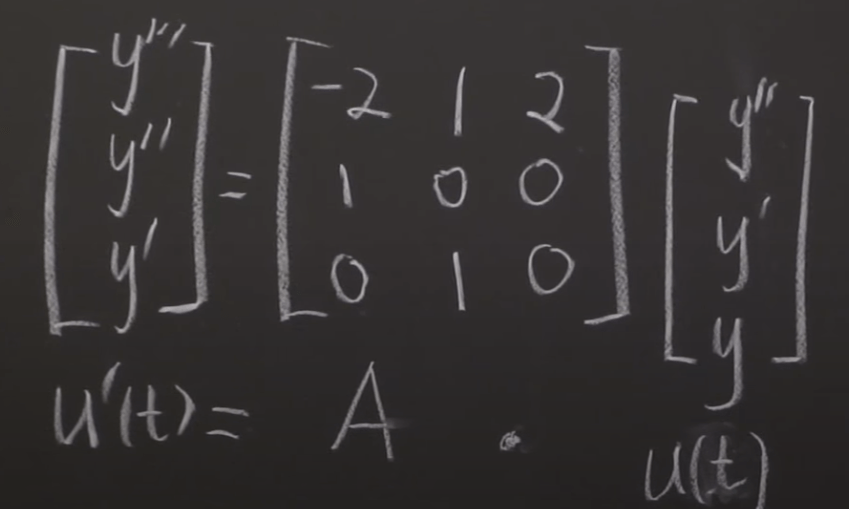
Then the problem is simply reduced to find the eigenvector and eigenvalues and then plug in the e to the lambda t exponential form.

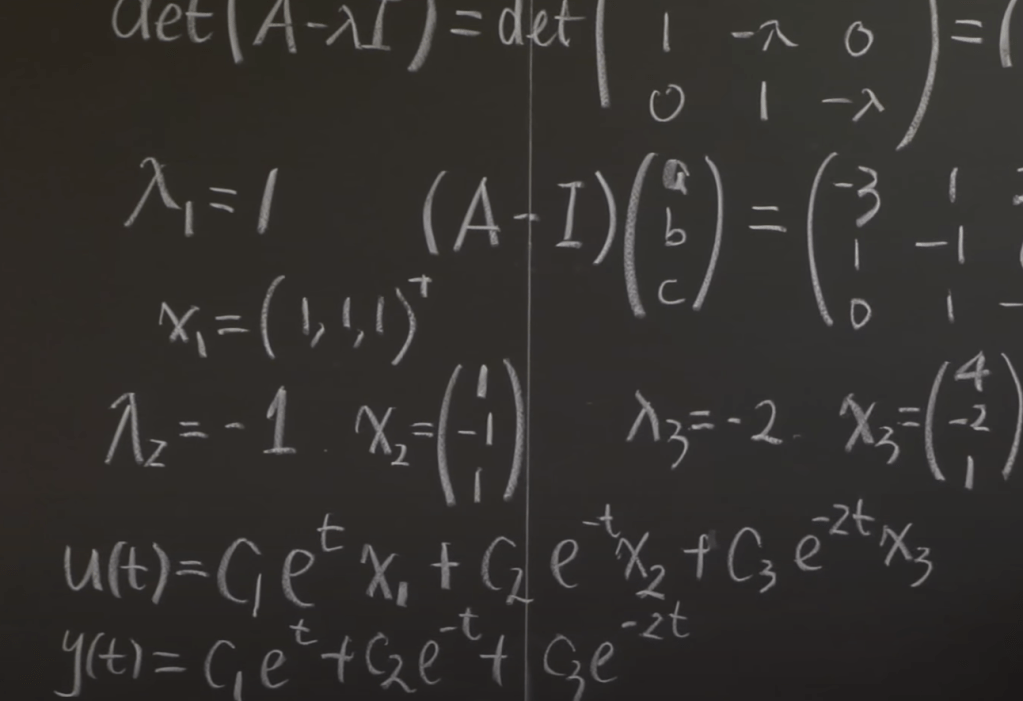
There is a second part of the problem:

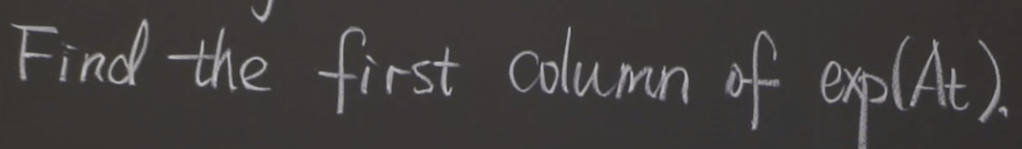
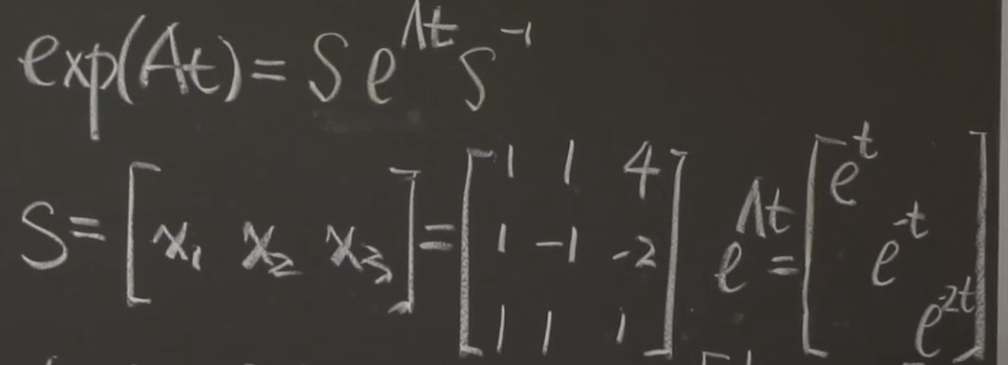
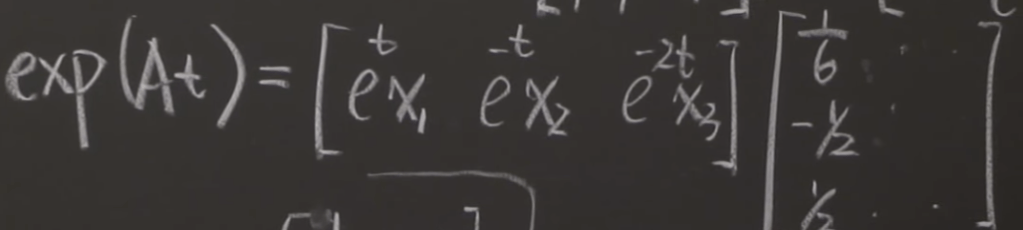
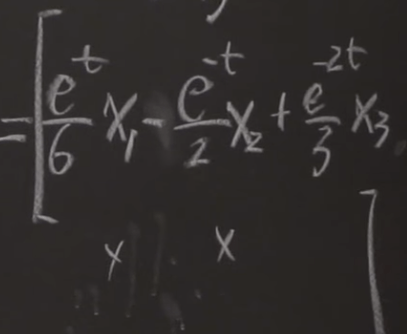
search the Math 113 Homework 8 Solutions.