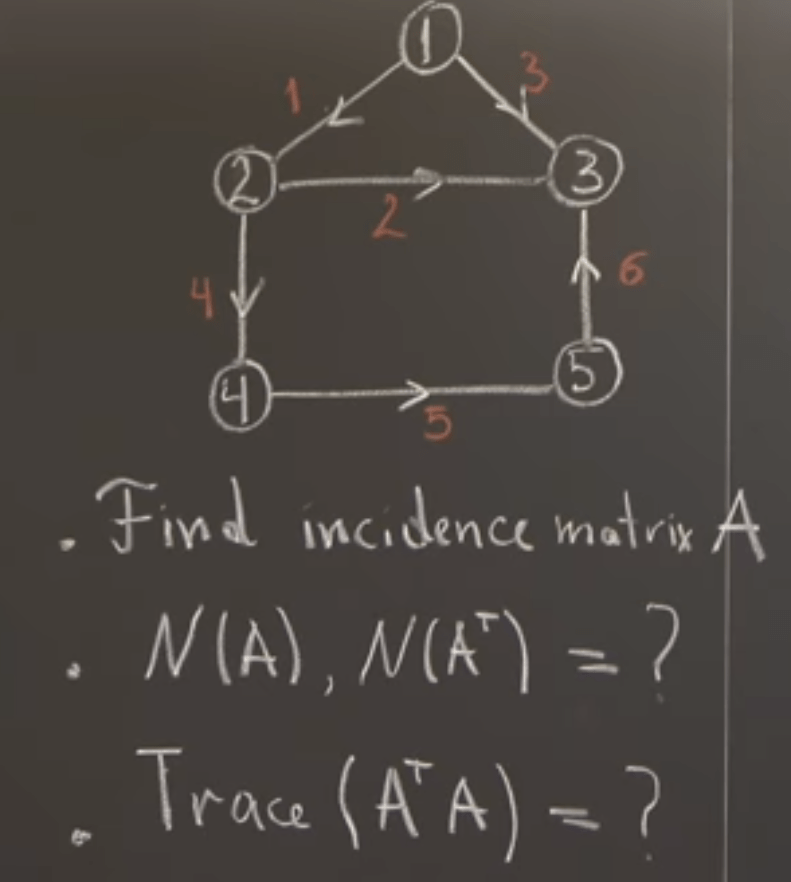
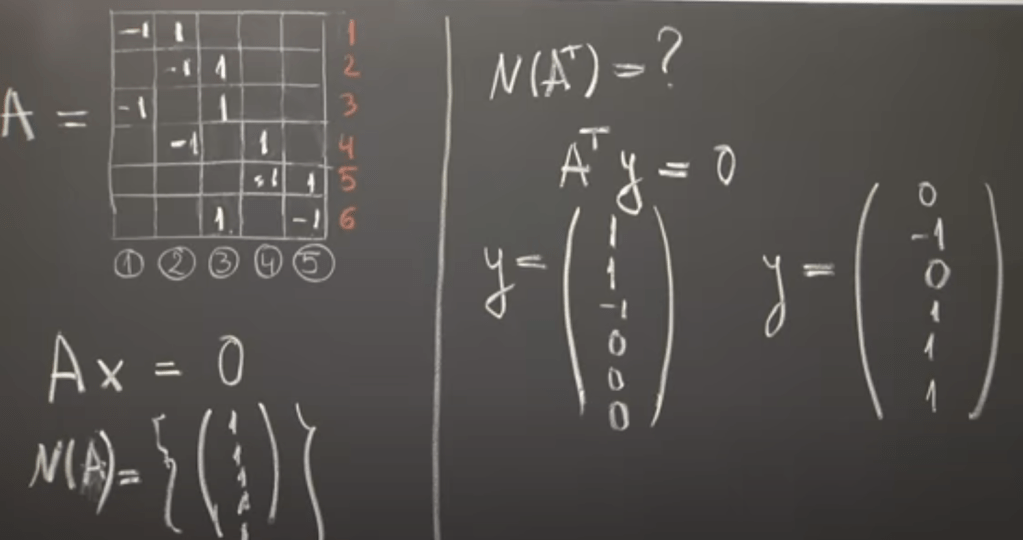If we have a network drawn in below graph:

to express it in Linear Algebra way

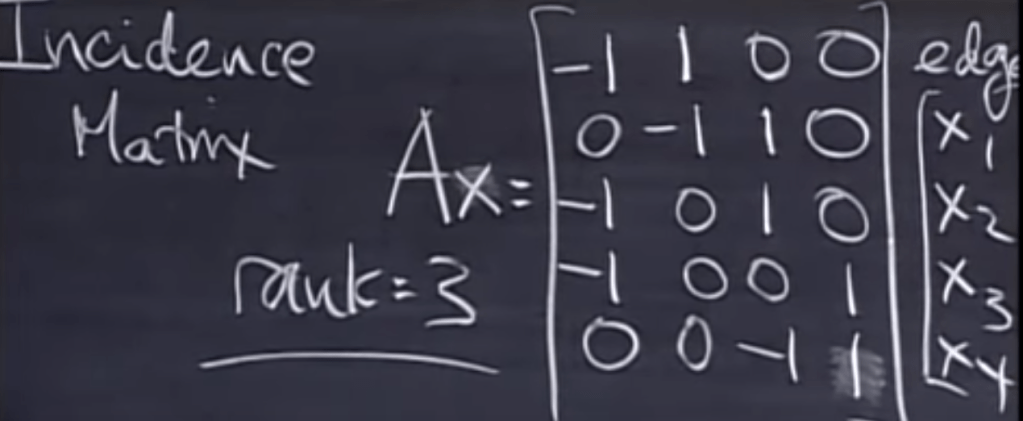
When we analyze the null space of this incidence matrix

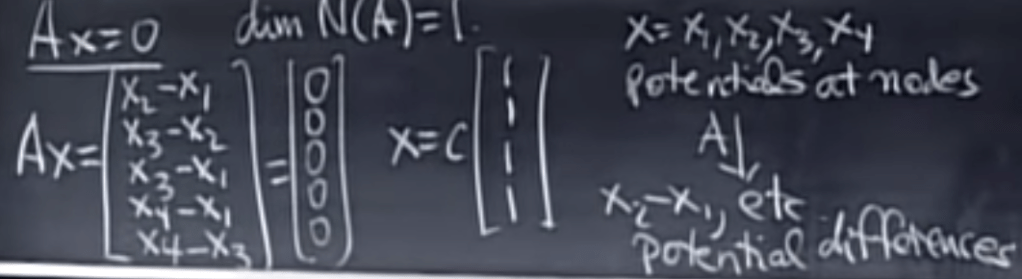
we can think of the nodes value as potentials at nodes. So if we set all potentials equal it forms the null space.

next to figure out the null space of transpose A:

Note the graph is

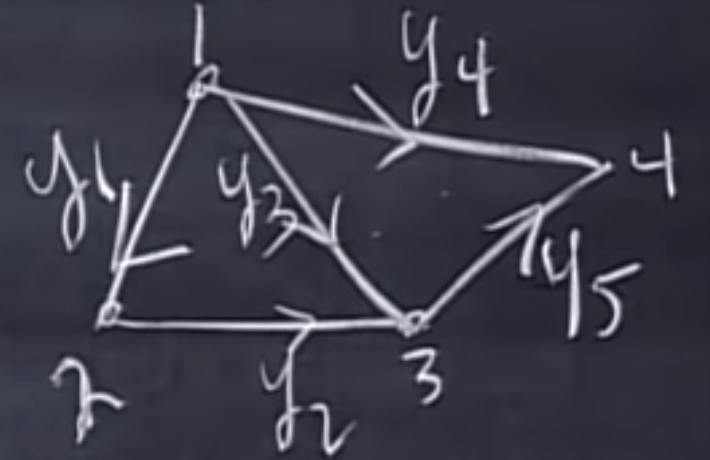
Then come up with the null space using the previous approach

A graph with no loops is called TREE.

so this leads to Euler’s formula again

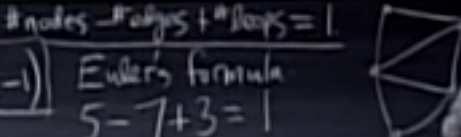
These graph theory in LA would be greatly useful in electric circuit computation in physics.

Practice problem