Dr.Strang’s explanation about projection matrix is the best.

Why do the mathematicians come up with such a concept “projection matrix”? It is to solve a universal and difficult problem – Ax=b, oftentimes, we can’t solve or can’t find the coefficient x that reside in column space of A to be b. So we have to approximate by finding Ax^ = p, where p is the closest vector to b.

So now the problem is to find the x hat in below equation, the key crux is to make b-p or b – Axhat perpendicular to the plane composed of two independent vector a1 and a2.

This is to solve

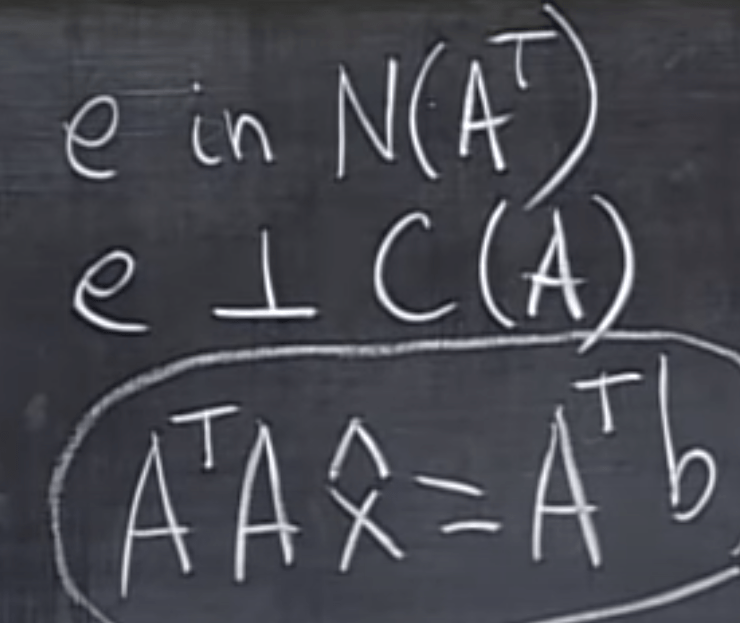
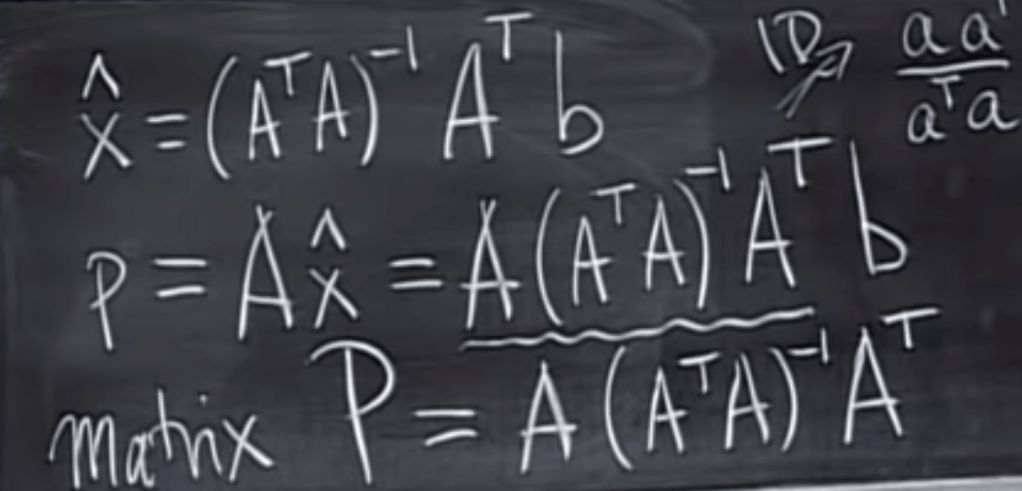
The matrix possess the properties of

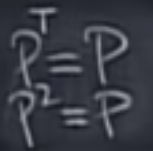
It’s much easier to use a line b projecting to a plane example as above. But Dr.Strang starts from looking at a vector b projecting on a single-directional line a, and inferred:

then if we define project p it has to be (a a^T/a^T a), the nominator is a matrix, while the denominator is a scaler.

they are consistent of course.

Reflecting on the spaces:

Next we have a good grasp of the projection matrix, we should apply it in “least square fitting by a line” classical problems everywhere.