How is Determinant derived? when we found the linearity between columns, the proportion leads to the Determinant computation. So we need ad-bc <> 0, which is the determinant cannot be zero for a matrix to be invertible.

The geometrical meaning of Determinant is that when transformed by the linear transformation/matrix, the scaled times is an absolute value which is determinant.

Dr.Strang just threw two properties up front: one is permutation (changing two rows of a square matrix, the sign of determinant changed) and the other is linearity (multiplying one row of a square matrix as follows).

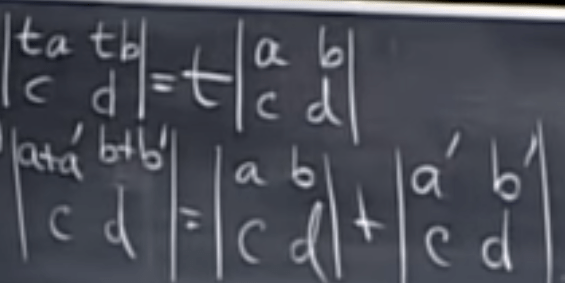
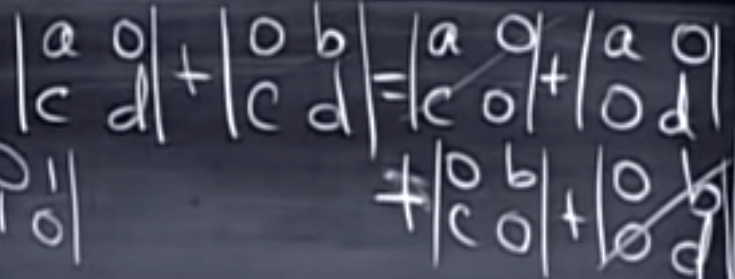
triangular matrix determinant is the production of the diagonals.

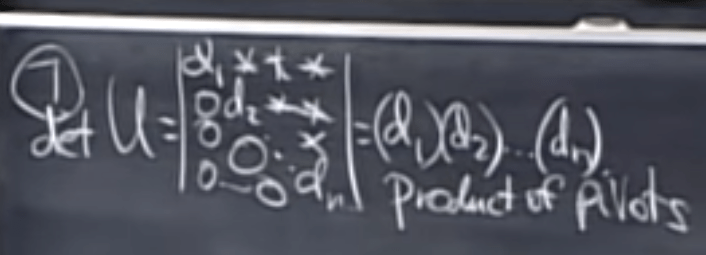
this can be inferred from above properties, and from this, we can also infer further that

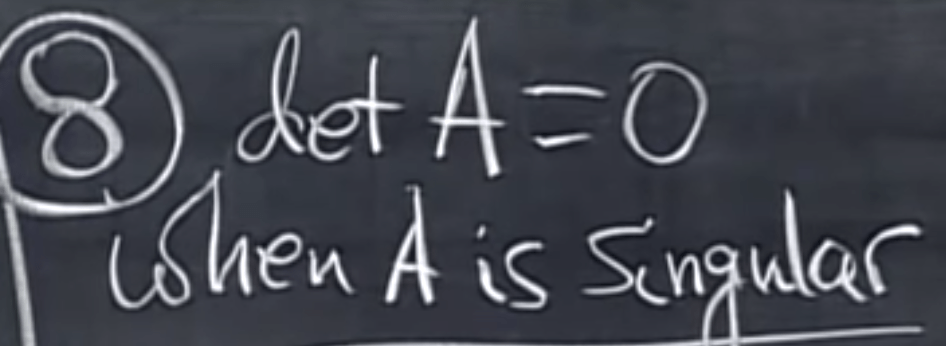
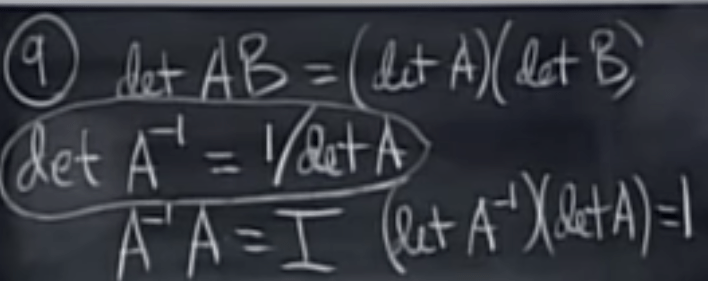
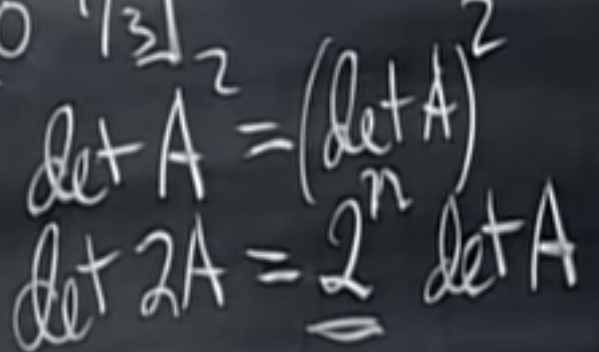
here is the practice problem set:

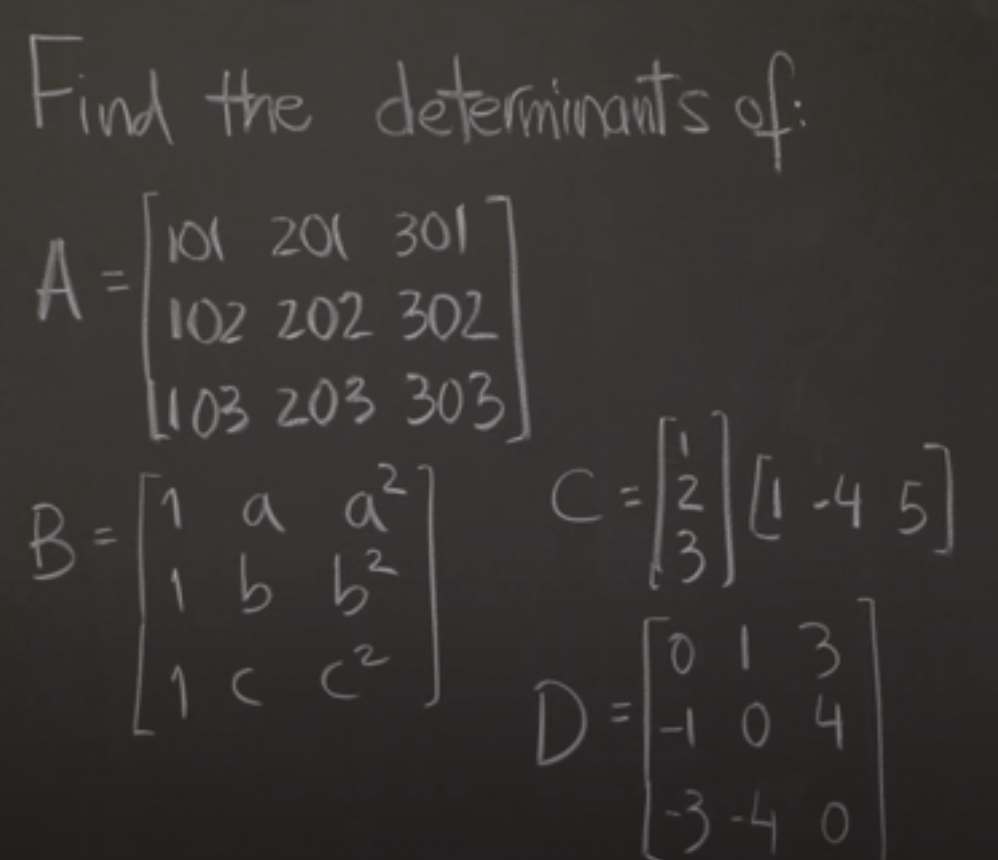
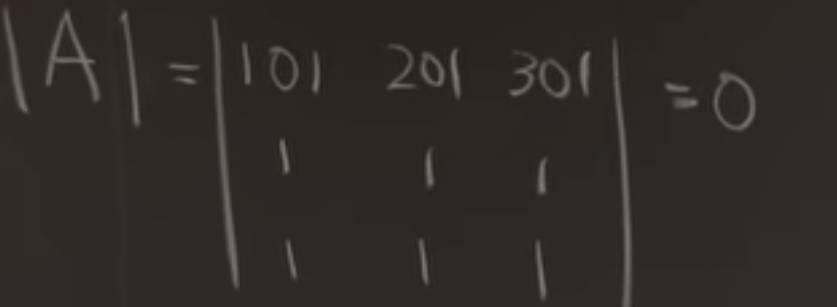
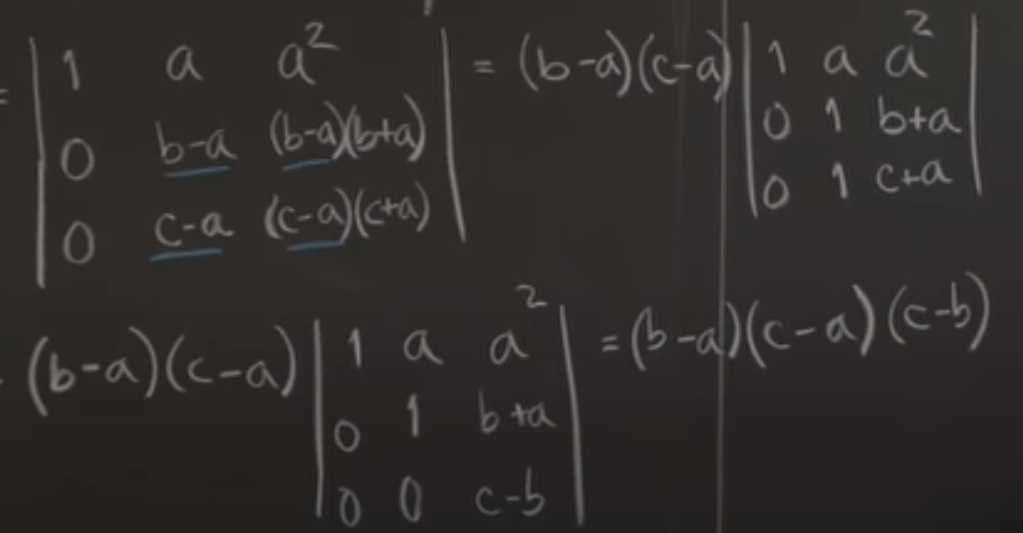
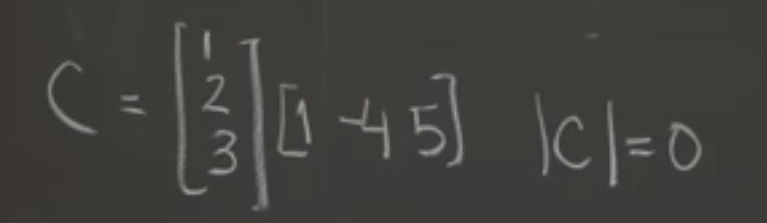
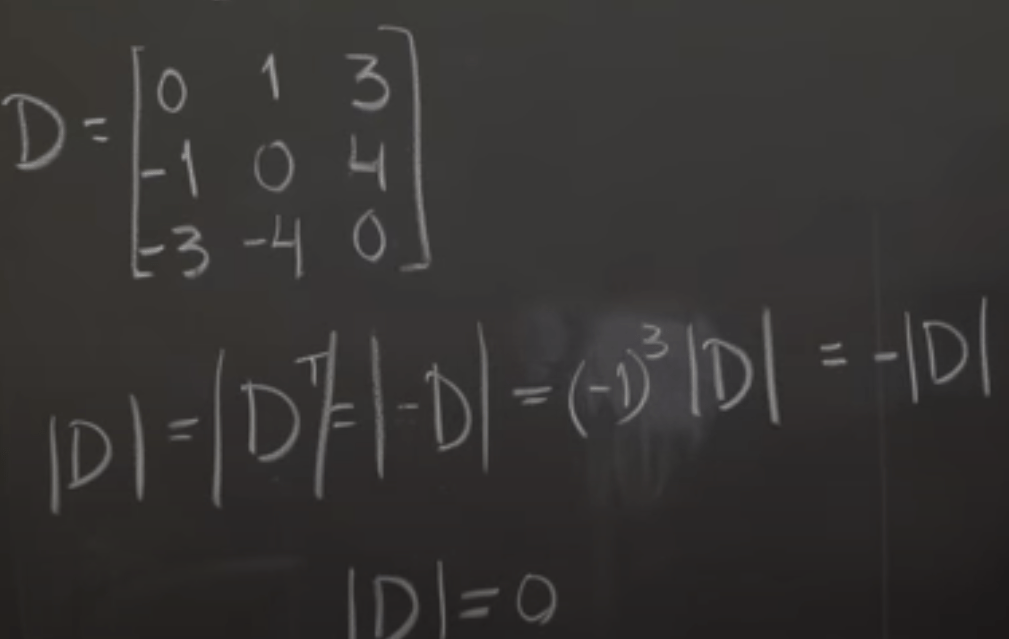
Use cofactor to calculate larger square matrix determinant.

Practice:

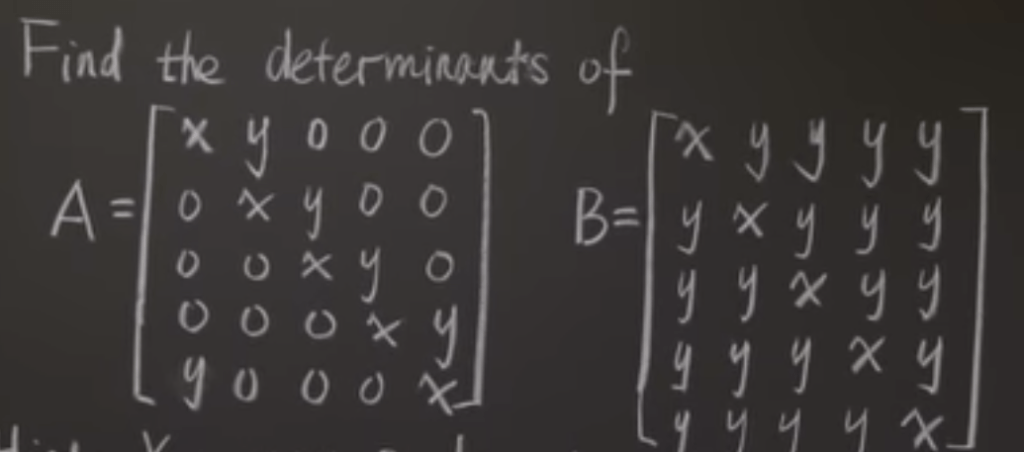
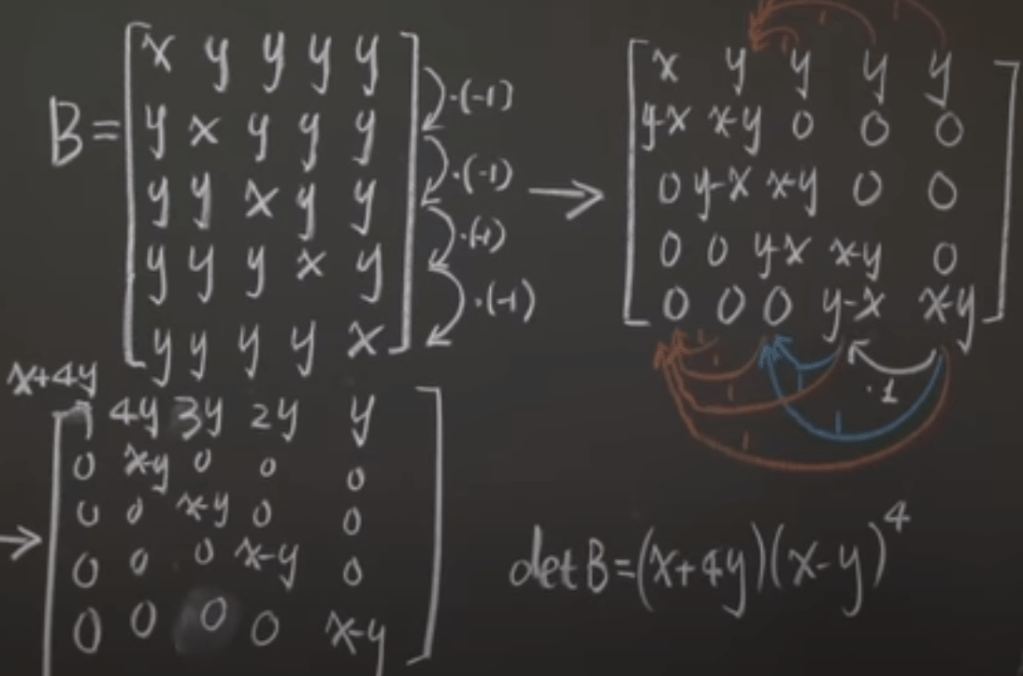
Applications of Determinant:

one is to find inverse:

then we can easily solve

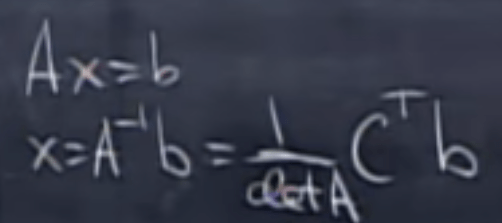
Another practice problem

Use determinant.

One thing not clear is why moving A3 to A3′ is just parallel moving relative to the base composed of O A1 and A2.