Why Matrix is so powerful in solving Differential problems(power series is another approach though)?!

Taking derivative of a function(vector) is equivalent to transform a function(vector), hence in ODE, taking one order of differentiation and get to itself is basically Ax =scaler*x, an eigenvector eigenvalue problem!

It can be multi-dimensional vector such as below 2-d linear system.

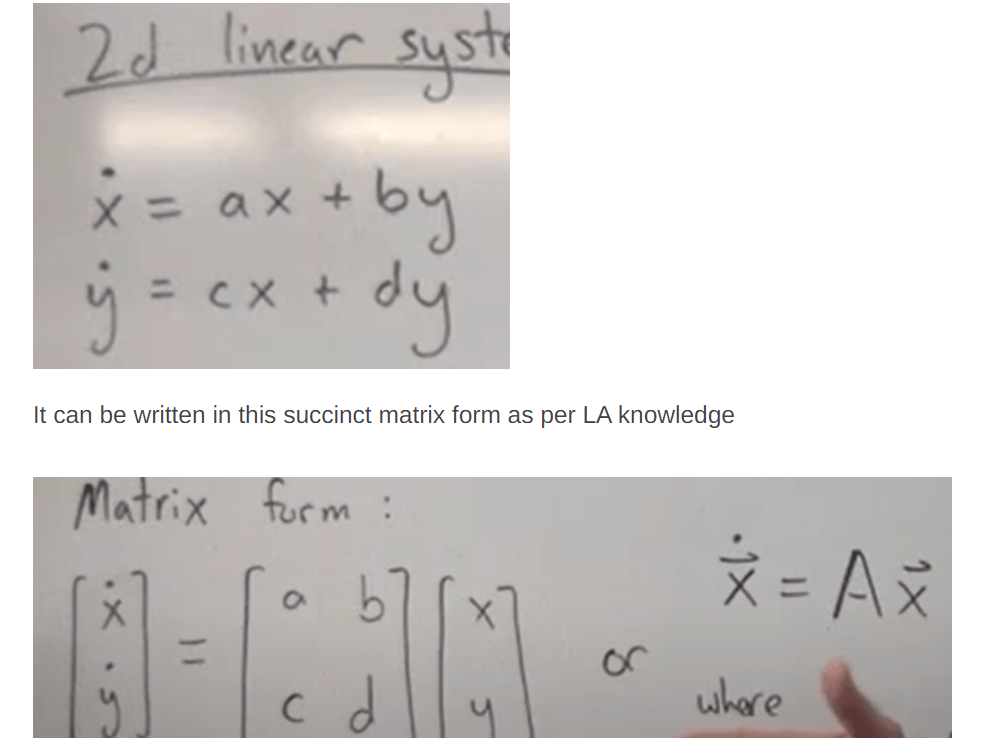
For higher order of differential problems, they can be reduced to above form, as higher order is just another dimension in Linear Algebra!

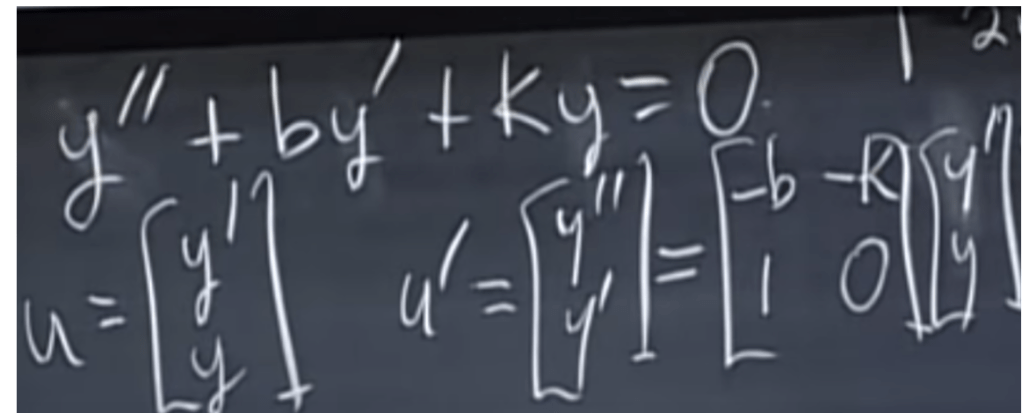
Hence if you are asked to solve below problem:

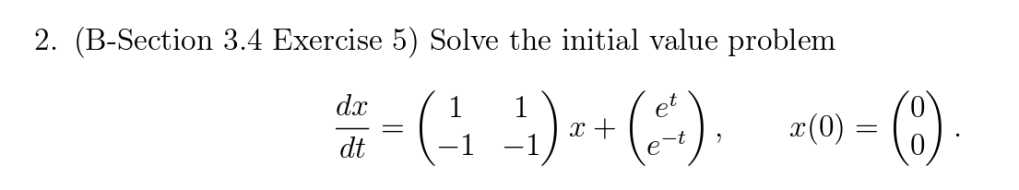
it’s exactly same as Ax=b problem, just Ax = nonhomogenous x’ with initial values given. And the solution can be referencing this blog. You guess out the general solution to be:

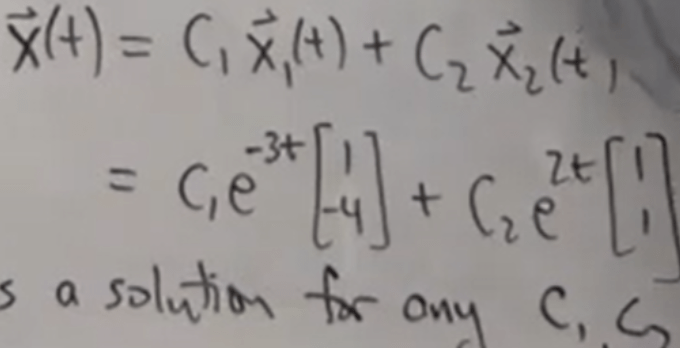
Not only Matrix is so powerful in solving Ax=b problem everywhere, it is also essential in solving difficult differential equations.

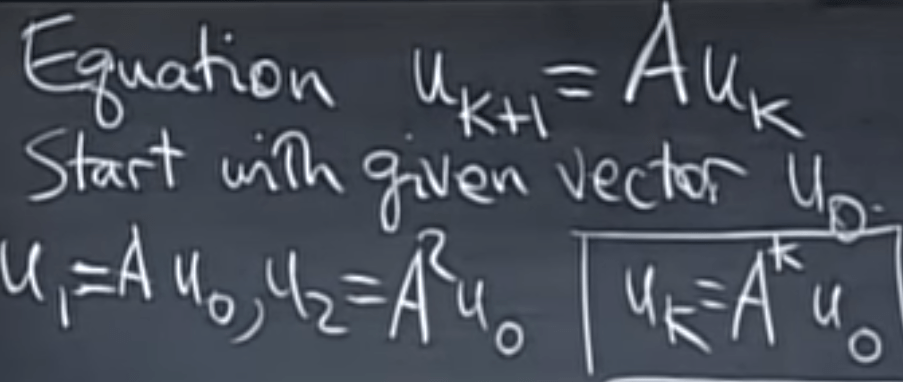
How?

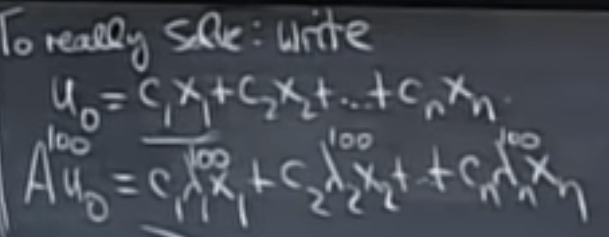
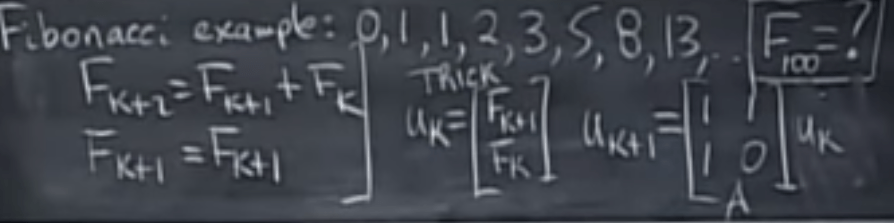
To apply this trick, let’s use Fibonacci numbers:

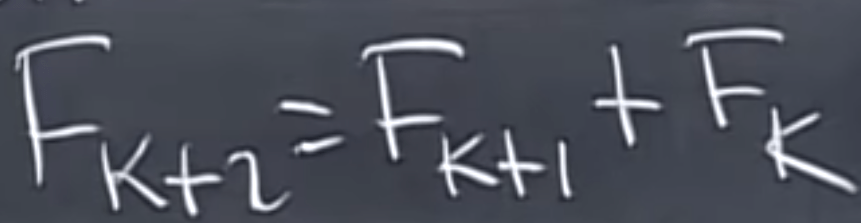
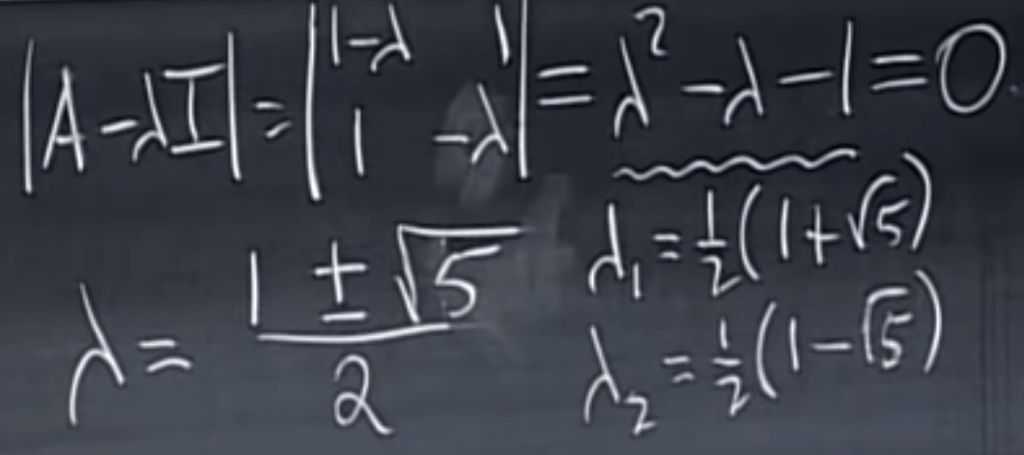
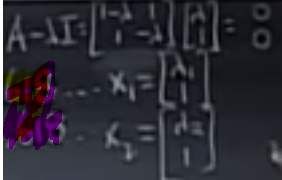
Practice problem

Following the same spirit of above Fibonacci sequence, try to solve general ODE:

The general solution would be

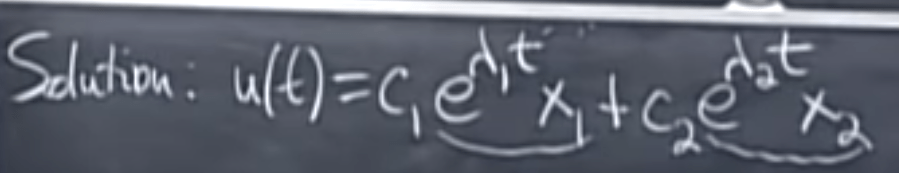
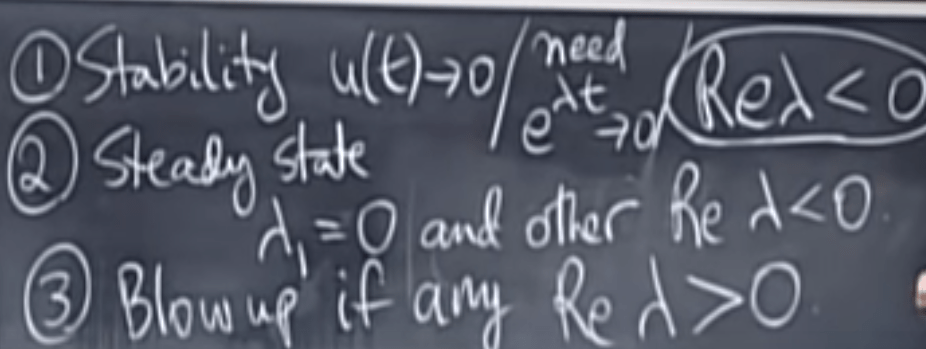
Now let’s deduce the power of powering matrix by setting u=Sv,

given

We can solve e^AT by Taylor Series:

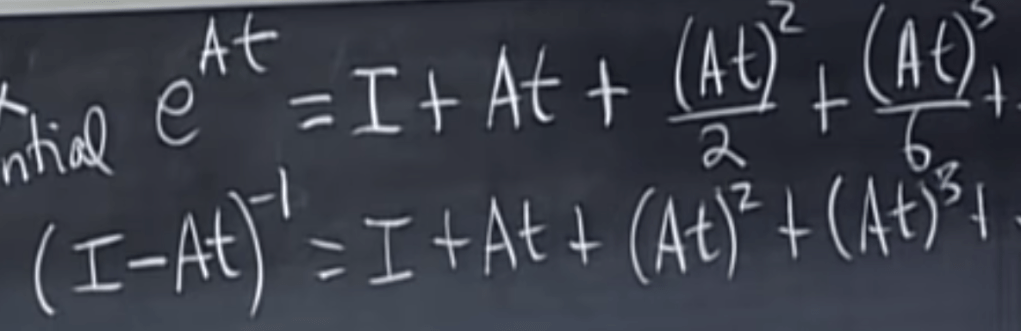
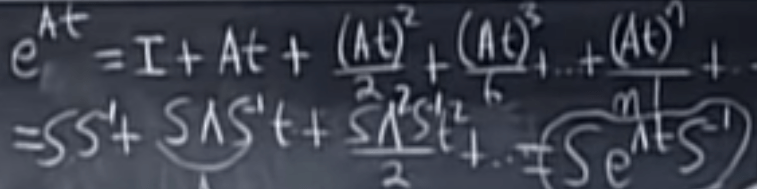
Plugged in A as the eigen diagonal matrix form

Note we can qualitatively evaluate if the equation goes to stability by the part of lambda, if in differential equation situation the real part of lambda has to be on the left side(negative), if in lambda power situation, then the lambda absolute value has to be within the circle.

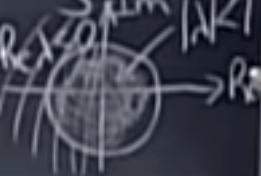
The profound application is to solve higher order of DEs, for instance:

This trick needs to be practiced over and over again:

reference link here.