What is familiar is full-rank/square matrix which has 2-side inverse:

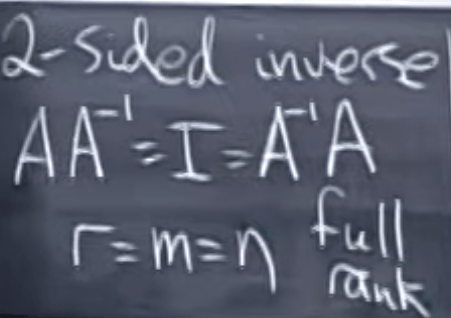
Now if the A has full column space, it has null null space and only have zero or one solution to Ax=b, we call the (A^TA)^-1A^T as left inverse to A. The identity is nxn matrix.

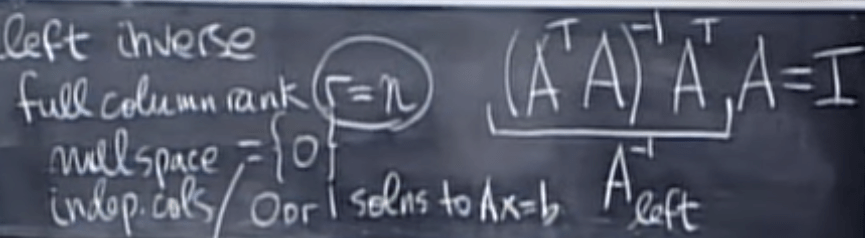
Flip side, the right inverse is

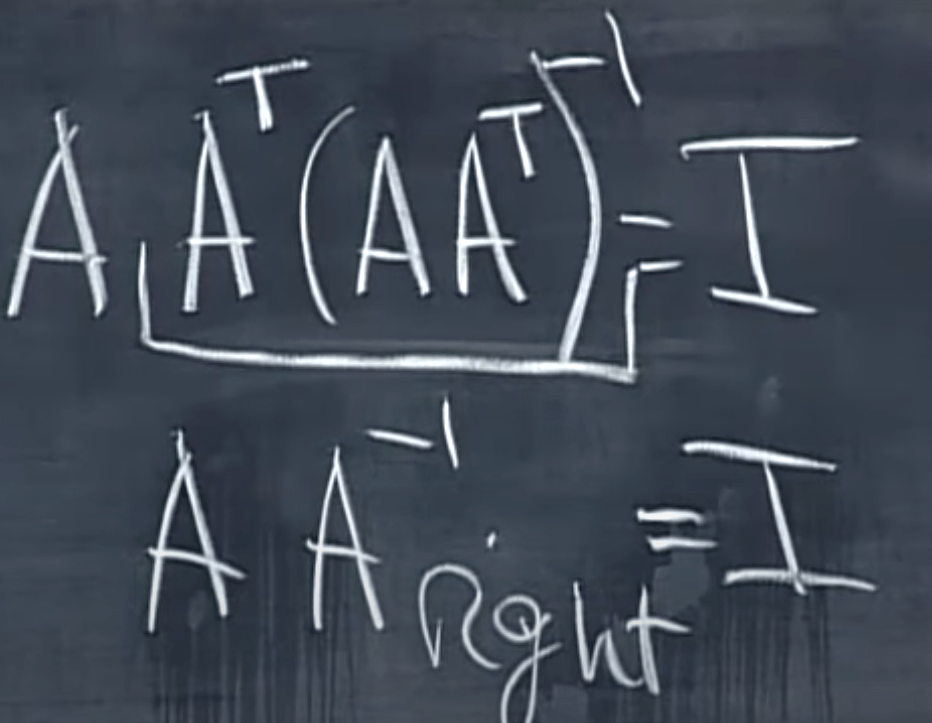
What if we rearrange the equation we get the following, this is the projection transform/matrix.

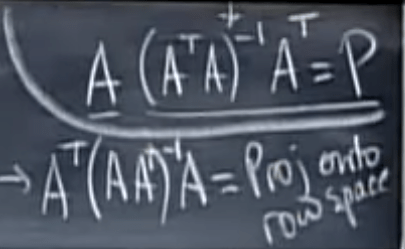
If there are two vectors in row space that are different then their mapping to column space Ax and Ay must be different two, as is proved below:

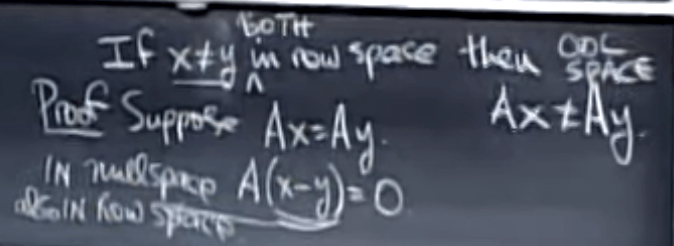
In mathematics, and in particular linear algebra, the Moore–Penrose inverse {\displaystyle A^{+}} of a matrix {\displaystyle A} is the most widely known generalization of the inverse matrix. A common use of the pseudoinverse is to compute a “best fit” (least squares) solution to a system of linear equations that lacks a solution (see below under § Applications). Another use is to find the minimum (Euclidean) norm solution to a system of linear equations with multiple solutions. 

Why it has application in SVD?

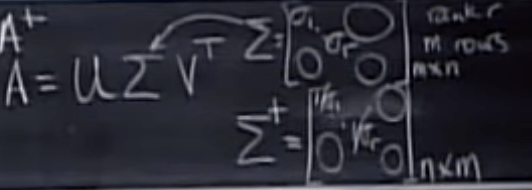
The pseudoinverse of diagonal matrix does not lead to identity(square) but the rectangular matrix looking like identity but with zero filled in, it’s a projection to row/column space.

to find pseudoinverse