I’ve been amazed by how smart people can solve puzzles, play Go now I am more amazed that this Reinforcement Learning math can crack any puzzle in a systematic way. this is the climax of artificial intelligence!

The key here is that machine is far better than human beings to recognize pattern/laws based on complex and gigantic data. So the real genius part is to systematically calculate and cumulate all the trial and error experience, and Markov Decision Making – all your decision is dependent on the previous state, even previous state is subsequent or caused by previous of previous.

In math language, terminology is condensed to policy, Q-value, value iteration/dynamic programing to realize the “thinking” process. One task for me is to grasp these RL “jargons”: policy is the agent’s behavior function, there are deterministic policy and stochastic policy;

value function measures how good each state and/or action is, for example, below equation shows the value function at state s for policy pie;

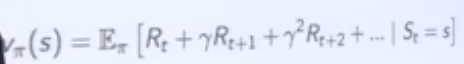
model is the agent’s representation of the environment:

Exploration is to try and get more information about the environment, exploitation is to exploit known information to maximize rewards.

Now to dive deeper. As mentioned above, one of the two key elements of RL is MDP Markov Decision Process. The below is the State Transition Matrix of Markov state:

Using this student Markov Chain as an example to illustrate

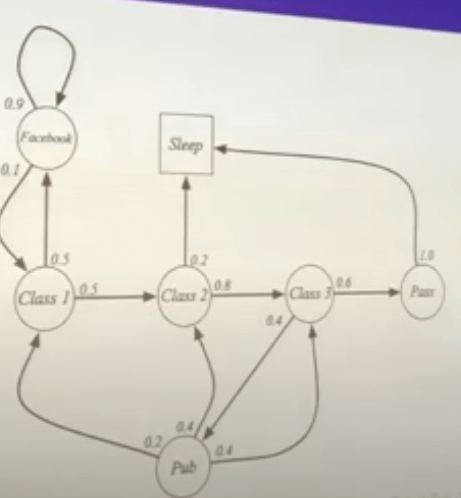
The State Transition Matrix is

Then we need to draw Markov Chain with Values, which is Markov Reward Process, it’s made up of tuples(S, P, R, r). S is a finite set of states, P is state transition probability matrix, Rs is the reward function at state s and r is the discount factor. So there are various routes the student can take, set starting state S1 = C1 and discount factor as 1/2, we can compute all the forward-looking rewards aggregation for each route.

The value function v at state s can always be decomposed to two parts: an immediate reward and a successor reward. This is where dynamic programming comes in naturally. And this is the famous Bellman Equation for MRPs.

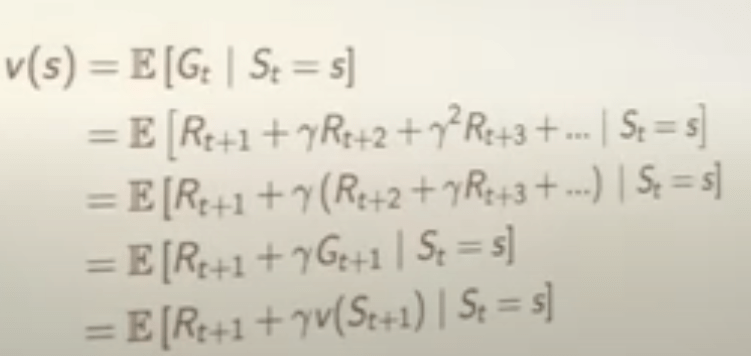
Or in another form

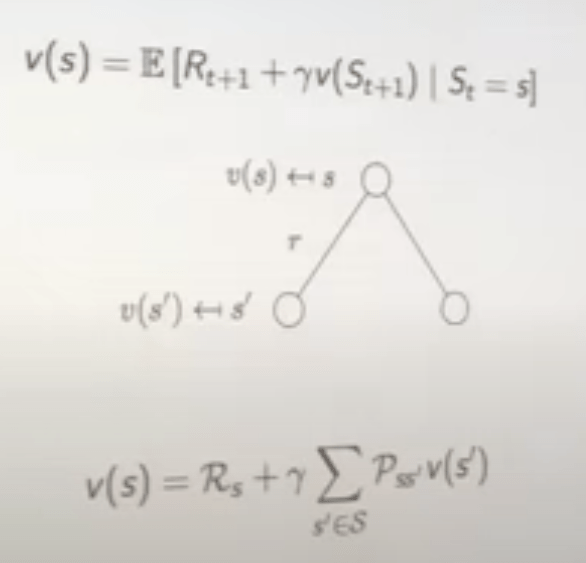
Policy is another important concept, above arrow figure roughly conveys the idea that policy dictates the action, to be more specific and accurate, policy is the distribution over actions given states, it is time-independent.

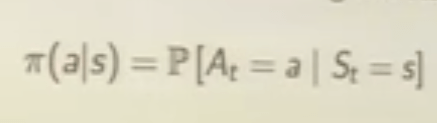
The above V(s) is agnostic of policy, while in solving real problem, policy is needed and hence the value function following a policy pie is also expected(aggregated then averaged) value given policy pie.

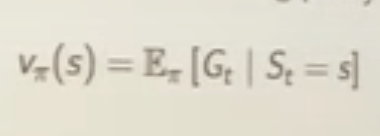
with the same logic, there is this action value function that is dependent on both pie and action taken a, it’s called q value.

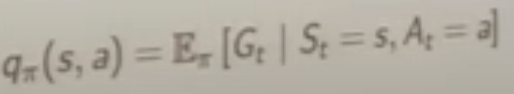
Lastly, we need to find the best behavior MDP-Optimal Value Realization.

The optimal state-value function is the maximum value function over all policies.

the optimal action-value function is the maximum action-value function over all policies. What leads to is actually what matters – optimal policy. An optimal policy can be found by maximizing over q star as shown below. and there is always a deterministic policy that is optimal.

So now the question is how to solve and find q star value, it is accomplished by Bellman Optimality Equation: