In relation to the zeroth-order logic in previous blog, this blog is about first order logic. According to wiki, First-order logic uses quantified variables over non-logical objects, and allows the use of sentences that contain variables, so that rather than propositions such as “Socrates is a man”, one can have expressions in the form “there exists x such that x is Socrates and x is a man”, where “there exists“ is a quantifier, while x is a variable.^[1] This distinguishes it from propositional logic, which does not use quantifiers or relations;^[2] in this sense, propositional logic is the foundation of first-order logic.

First-order logic is the standard for the formalization of mathematics into axioms, and is studied in the foundations of mathematics. Peano arithmetic and Zermelo–Fraenkel set theory are axiomatizations of number theory and set theory, respectively, into first-order logic. 

Notation is a critical part in learning logic. Logical Connectiveness are: ∧ for conjunction, ∨ for disjunction, → for implication, ↔ for biconditional, ¬ for negation

There are constant a, b, c; variables x, y, z, and predicates symbols are F, Q, R, S. if a = John, F = funny, then Fa means John is funny, while Fy means someone y is funny. R could be “funnier than”, so Fab means a is “funnier than” b.

There are existential quantifier and universal quantifier.

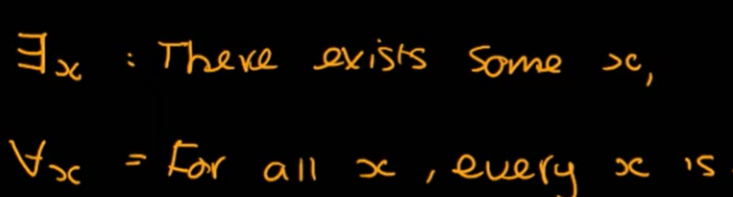
with these weapons, now one can express in logic symbols of the semantic meaning, such as “All teachers are happy”, we use H predicate symbol as happy, T as teacher, so succinctly it is

Relations are key in propositional logic, also in first-order logic, there are several types: reflective and symmetrical:

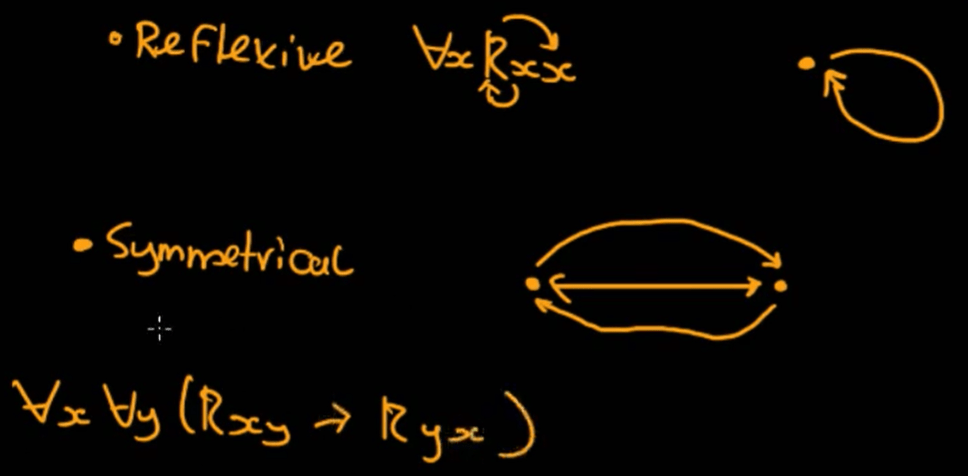
There can also be transitive:

To make maximum usage of all these symbols, we definitely need to know the 4 rules of equivelance:

Connecting all above equivalence rules, we can deduce

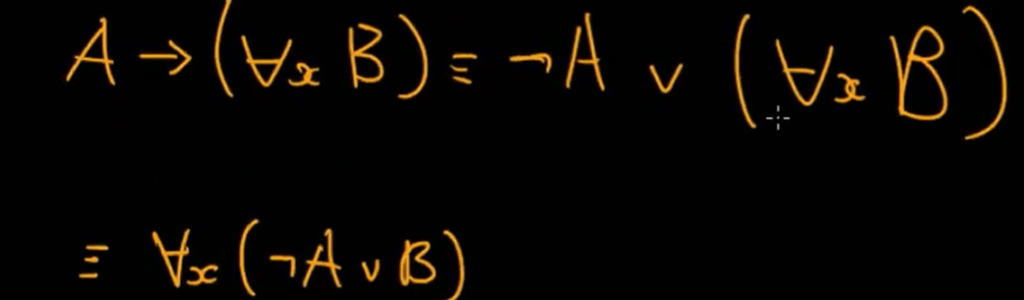
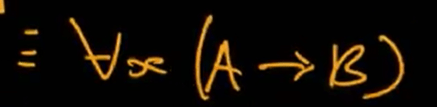
This naturally leads to prenex form such as below

There is an easy-to-make-mistake in moving quantifier ahead/prenex form

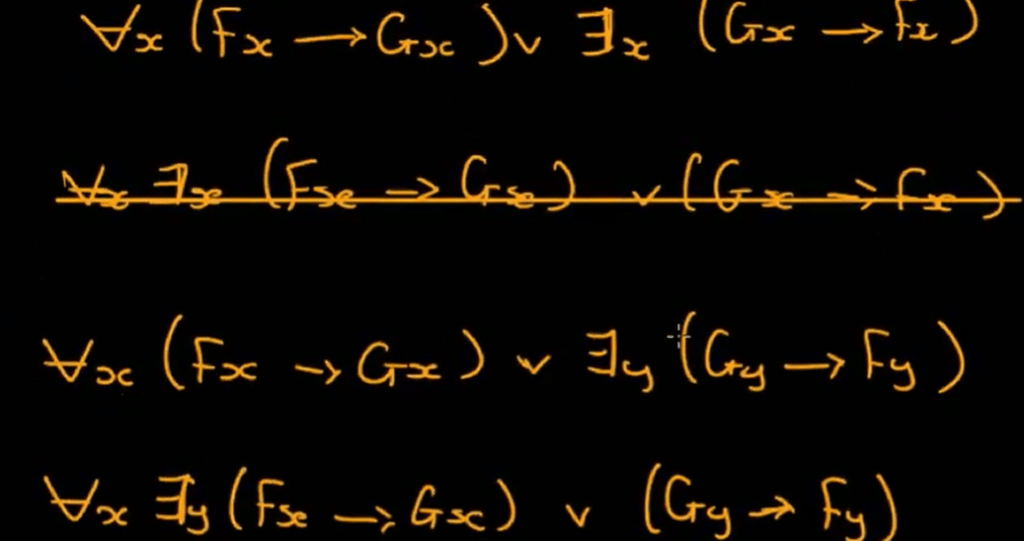
Lastly, we do a proof-tree example:

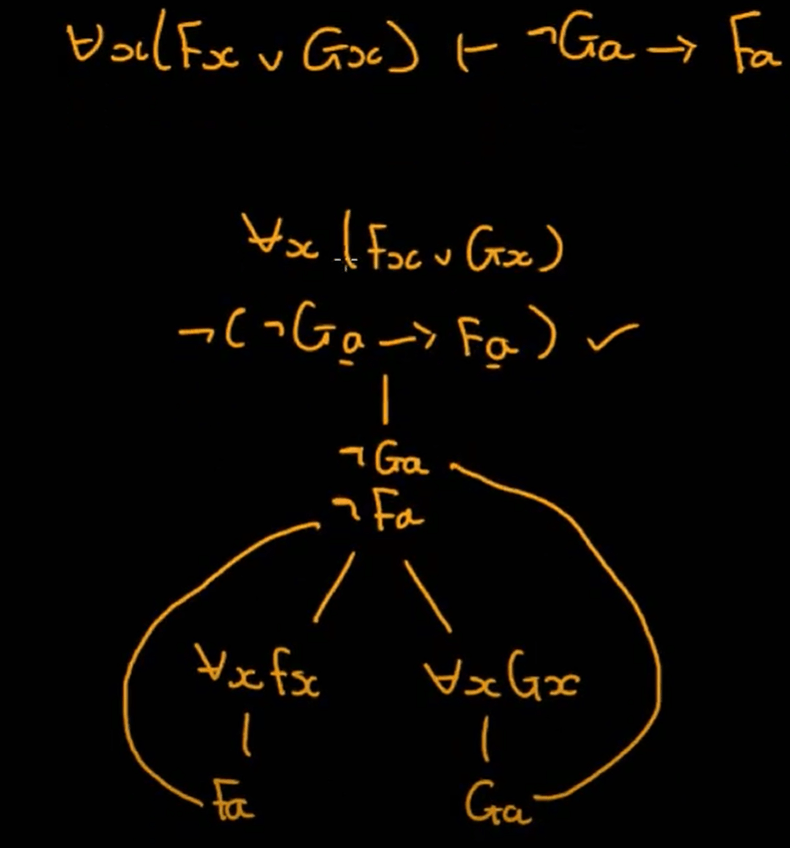
These clear intro of basic first-order logic is lectured by The Philosophy Academy