Sebastian is brilliant to explain this A* algorithm far better than academic which takes hours. The problem in simple form is like below, you need to find the optimal path from A to B. The natural resort is to use A* search algorithm.

What is A* algorithm, according to wiki, “A* (pronounced “A-star”) is a graph traversal and path searchalgorithm, which is often used in many fields of computer science due to its completeness, optimality, and optimal efficiency.^[1] One major practical drawback is its {\displaystyle O(b^{d})} space complexity, as it stores all generated nodes in memory. Thus, in practical travel-routing systems, it is generally outperformed by algorithms which can pre-process the graph to attain better performance,^[2] as well as memory-bounded approaches; however, A* is still the best solution in many cases”. It can be seen as an extension of Dijkstra’s algorithm. A* achieves better performance by using heuristics to guide its search.

Here is the way it works: for each node starting from A, calculating all its surrounding nodes with G cost, H cost and F cost. Then pick the ones that have the lowest F cost.

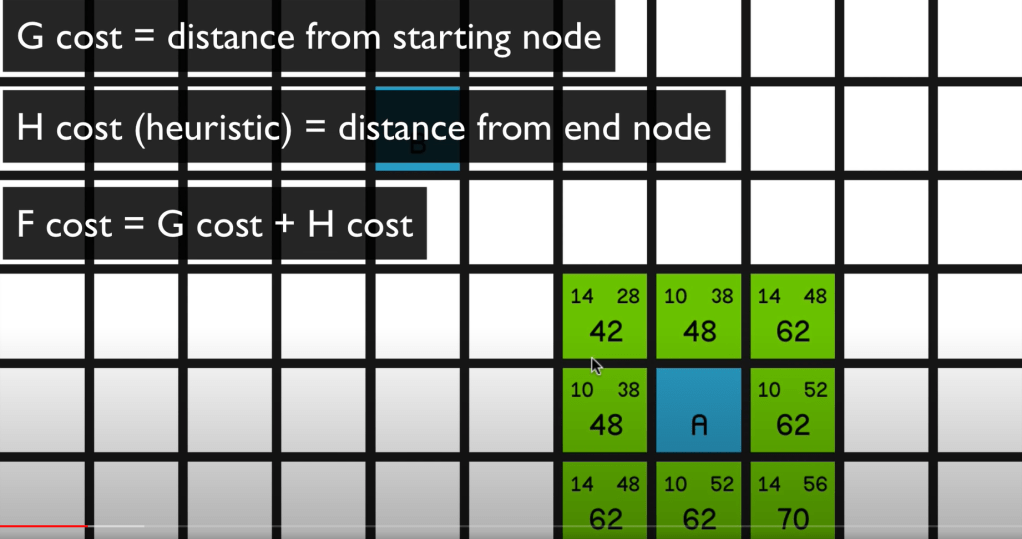
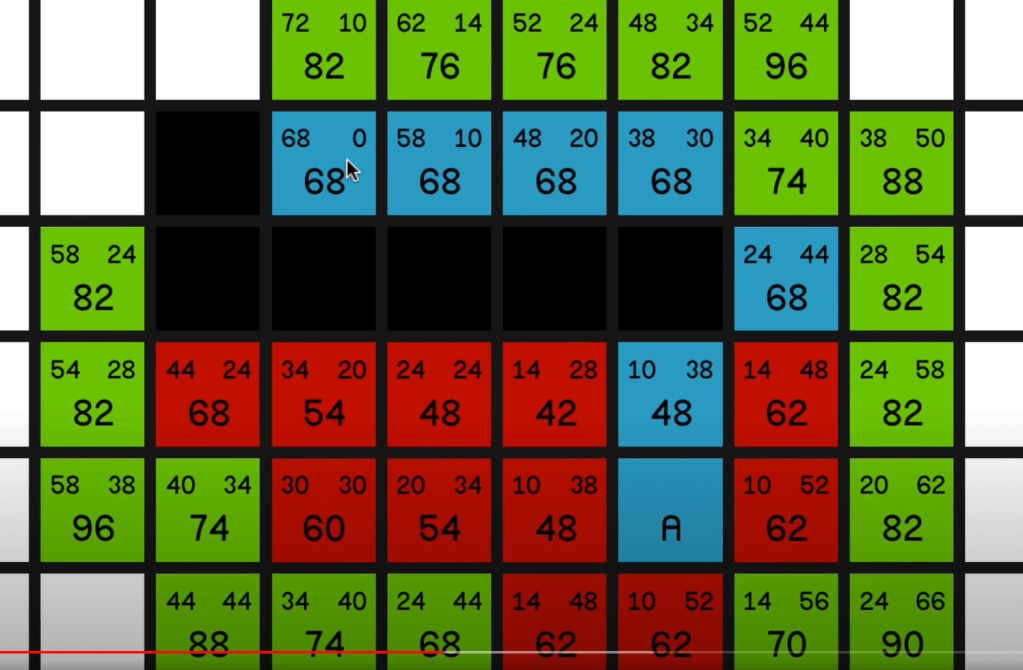
However what if there are obstacles like the black blocks in below graph, we need to continue exploring like we play the mining game of Microsoft, until we obtain the optimal path as shown in blue color. Note the value of G, H, and F cost keep updating along the way.

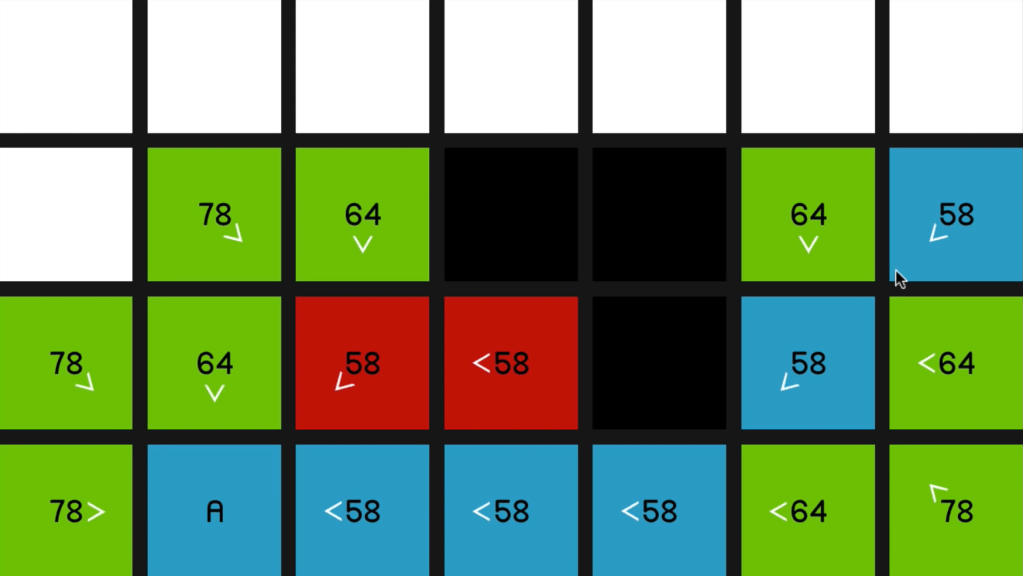
Next shows a shorthand to show the F cost value and figure out the path too.

To realize above the pseudocodes by Sebastian is

# A* Search Algorithm path finding pseudocodes
OPEN //the set of nodes to be evaluated
CLOSED //the set of nodes already evaluated
add the start node to OPEN
 
loop
        current = node in OPEN with the lowest f_cost
        remove current from OPEN
        add current to CLOSED
 
        if current is the target node //path has been found
                return
 
        foreach neighbour of the current node
                if neighbour is not traversable or neighbour is in CLOSED
                        skip to the next neighbour
 
                if new path to neighbour is shorter OR neighbour is not in OPEN
                        set f_cost of neighbour
                        set parent of neighbour to current
                        if neighbour is not in OPEN
                                add neighbour to OPEN