Constraint Satisfaction is the process of finding a solution through a set of constraints that impose conditions that the variables must satisfy. The optimization problem is related to constraint satisfaction from viewing CS definition. Per wiki page, Constraint satisfaction problems on finite domains are typically solved using a form of search. The most used techniques are variants of backtracking, constraint propagation, and local search. These techniques are used on problems with nonlinear constraints. Variable elimination and the simplex algorithm are used for solving linear and polynomial equations and inequalities, and problems containing variables with infinite domain. These are typically solved as optimization problems in which the optimized function is the number of violated constraints.

Following John Levin to grasp Constraint Satisfaction problems.

AC-3 algorithm (short for Arc Consistency Algorithm #3) is one of a series of algorithms used for the solution of constraint satisfaction problems (or CSP’s). The vivid demo by John Levin is here.

1. Tune each binary constraint into two arc e.g. A <> B become A<>B and B<>A
2. Add all the arcs to an agenda
3. Repeat until agenda is empty

• take an arc (Xi, Xj) off the agenda and check it
• for every value of Xi, there must be some value of Xj
• remove any misconsistent values from Xi
• if Xi has changed, add all arcs of the form (Xk, Xi) to the agenda

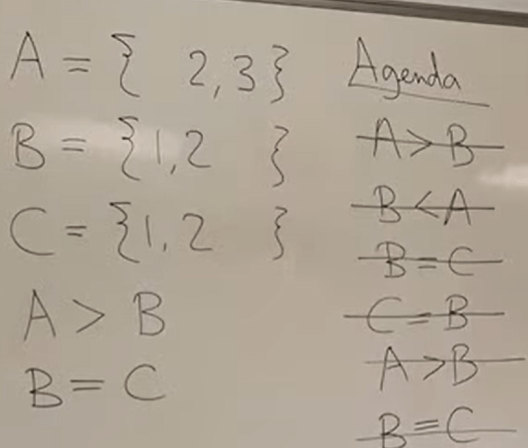
 Input:
   A set of variables X
   A set of domains D(x) for each variable x in X. D(x) contains vx0, vx1... vxn, the possible values of x
   A set of unary constraints R1(x) on variable x that must be satisfied
   A set of binary constraints R2(x, y) on variables x and y that must be satisfied
   
 Output:
   Arc consistent domains for each variable.
 
 function ac3 (X, D, R1, R2)
     // Initial domains are made consistent with unary constraints.
     for each x in X
         D(x) := { vx in D(x) | vx satisfies R1(x) }   
     // 'worklist' contains all arcs we wish to prove consistent or not.
     worklist := { (x, y) | there exists a relation R2(x, y) or a relation R2(y, x) }
 
     do
         select any arc (x, y) from worklist
         worklist := worklist - (x, y)
         if arc-reduce (x, y) 
             if D(x) is empty
                 return failure
             else
                 worklist := worklist + { (z, x) | z != y and there exists a relation R2(x, z) or a relation R2(z, x) }
     while worklist not empty
 
 function arc-reduce (x, y)
     bool change = false
     for each vx in D(x)
         find a value vy in D(y) such that vx and vy satisfy the constraint R2(x, y)
         if there is no such vy {
             D(x) := D(x) - vx
             change := true
         }
     return change