There are some NP problems (nondeterministic problems) that we will apply SA (simulated annealing) algorithms, Genetic Algorithms etc. to solve. The key is to overcome being stuck in a local area. Simulated Annealing allows several testing leaps in the beginning so the probability of reaching a global minimum or maximum is high.

Whether to continue exploring, SA needs to compute a probability score, from equation below, one can see a higher temperature or smaller loss will cause higher probability.

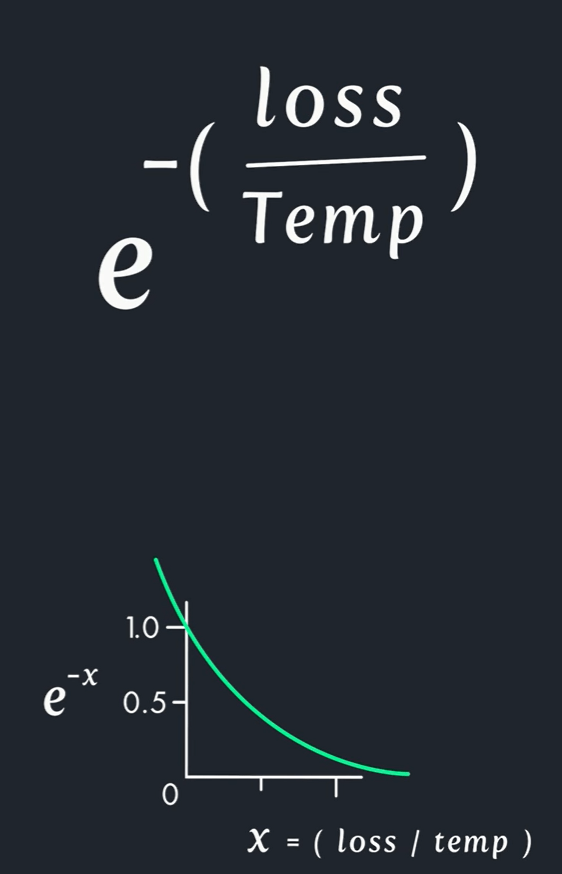
The python codes as

# Simulated Annealing
import numpy as np
import matplotlib.pyplot as plt

def h(x):
    if x < -1 or x > 1:
        y = 0
    else:
        y = (np.cos(50*x) + np.sin(20*x))
    return y

hv = np.vectorize(h)
X = np.linspace(-1, 2, num=1000)
plt.plot(X, hv(X))
plt.show()
# simple greedy search will stop at a local minmum or maxmum
def simple_greedy_search(func, start=0, N=100):
    x = start
    history = []
    for i in range(N):
        history.append(x) # keep track of steps
        u = 0.001 #np.random.rand() #some noise
        xleft, xright = x-u, x+u #look around the neighborhood
        yleft, yright = func(xleft), func(xright)
        if yleft > yright:
            x = xleft
        else:
            x = xright
    return x, history
x0, history = simple_greedy_search(hv, start=-0.02, N=100)
# here is the simulated annealing algorithm
def SA(search_space, func, T):
    scale = np.sqrt(T) 
    start = np.random.choice(search_space)
    x = start * 1
    cur = func(x)
    history = [x]
    for i in range(1000):
        prop = x + np.random.normal()*scale #.uniform(-1, 1, size=1) *scale
        if prop > 1 or prop < 0 or np.log(np.random.rand()) * T > (func(prop) - cur):
            prop = x
        x = prop
        cur = func(x)
        T = 0.9 * T # reduce temperature by 10% each iteration
        history.append(x)
    return x, history

SA is so powerful that those NP problems such as TSP(traveling salesman problem), Sudoku and Rubik problems can be systematically solved by SA.

below are the python codes to use SA solving Sudoku by ChallengingLuck

# Simulated Annealing (SA) techqnique to solve Sudoku posted by challengingLuck
import random
import numpy as np
import math 
from random import choice
import statistics 

startingSudoku = """
                    024007000
                    600000000
                    003680415
                    431005000
                    500000032
                    790000060
                    209710800
                    040093000
                    310004750
                """

sudoku = np.array([[int(i) for i in line] for line in startingSudoku.split()])

def PrintSudoku(sudoku):
    print("\n")
    for i in range(len(sudoku)):
        line = ""
        if i == 3 or i == 6:
            print("---------------------")
        for j in range(len(sudoku[i])):
            if j == 3 or j == 6:
                line += "| "
            line += str(sudoku[i,j])+" "
        print(line)

def FixSudokuValues(fixed_sudoku):
    for i in range (0,9):
        for j in range (0,9):
            if fixed_sudoku[i,j] != 0:
                fixed_sudoku[i,j] = 1
    
    return(fixed_sudoku)

# Cost Function    
def CalculateNumberOfErrors(sudoku):
    numberOfErrors = 0 
    for i in range (0,9):
        numberOfErrors += CalculateNumberOfErrorsRowColumn(i ,i ,sudoku)
    return(numberOfErrors)

def CalculateNumberOfErrorsRowColumn(row, column, sudoku):
    numberOfErrors = (9 - len(np.unique(sudoku[:,column]))) + (9 - len(np.unique(sudoku[row,:])))
    return(numberOfErrors)


def CreateList3x3Blocks ():
    finalListOfBlocks = []
    for r in range (0,9):
        tmpList = []
        block1 = [i + 3*((r)%3) for i in range(0,3)]
        block2 = [i + 3*math.trunc((r)/3) for i in range(0,3)]
        for x in block1:
            for y in block2:
                tmpList.append([x,y])
        finalListOfBlocks.append(tmpList)
    return(finalListOfBlocks)

def RandomlyFill3x3Blocks(sudoku, listOfBlocks):
    for block in listOfBlocks:
        for box in block:
            if sudoku[box[0],box[1]] == 0:
                currentBlock = sudoku[block[0][0]:(block[-1][0]+1),block[0][1]:(block[-1][1]+1)]
                sudoku[box[0],box[1]] = choice([i for i in range(1,10) if i not in currentBlock])
    return sudoku

def SumOfOneBlock (sudoku, oneBlock):
    finalSum = 0
    for box in oneBlock:
        finalSum += sudoku[box[0], box[1]]
    return(finalSum)

def TwoRandomBoxesWithinBlock(fixedSudoku, block):
    while (1):
        firstBox = random.choice(block)
        secondBox = choice([box for box in block if box is not firstBox ])

        if fixedSudoku[firstBox[0], firstBox[1]] != 1 and fixedSudoku[secondBox[0], secondBox[1]] != 1:
            return([firstBox, secondBox])

def FlipBoxes(sudoku, boxesToFlip):
    proposedSudoku = np.copy(sudoku)
    placeHolder = proposedSudoku[boxesToFlip[0][0], boxesToFlip[0][1]]
    proposedSudoku[boxesToFlip[0][0], boxesToFlip[0][1]] = proposedSudoku[boxesToFlip[1][0], boxesToFlip[1][1]]
    proposedSudoku[boxesToFlip[1][0], boxesToFlip[1][1]] = placeHolder
    return (proposedSudoku)

def ProposedState (sudoku, fixedSudoku, listOfBlocks):
    randomBlock = random.choice(listOfBlocks)

    if SumOfOneBlock(fixedSudoku, randomBlock) > 6:  
        return(sudoku, 1, 1)
    boxesToFlip = TwoRandomBoxesWithinBlock(fixedSudoku, randomBlock)
    proposedSudoku = FlipBoxes(sudoku,  boxesToFlip)
    return([proposedSudoku, boxesToFlip])

def ChooseNewState (currentSudoku, fixedSudoku, listOfBlocks, sigma):
    proposal = ProposedState(currentSudoku, fixedSudoku, listOfBlocks)
    newSudoku = proposal[0]
    boxesToCheck = proposal[1]
    currentCost = CalculateNumberOfErrorsRowColumn(boxesToCheck[0][0], boxesToCheck[0][1], currentSudoku) + CalculateNumberOfErrorsRowColumn(boxesToCheck[1][0], boxesToCheck[1][1], currentSudoku)
    newCost = CalculateNumberOfErrorsRowColumn(boxesToCheck[0][0], boxesToCheck[0][1], newSudoku) + CalculateNumberOfErrorsRowColumn(boxesToCheck[1][0], boxesToCheck[1][1], newSudoku)
    # currentCost = CalculateNumberOfErrors(currentSudoku)
    # newCost = CalculateNumberOfErrors(newSudoku)
    costDifference = newCost - currentCost
    rho = math.exp(-costDifference/sigma)
    if(np.random.uniform(1,0,1) < rho):
        return([newSudoku, costDifference])
    return([currentSudoku, 0])


def ChooseNumberOfItterations(fixed_sudoku):
    numberOfItterations = 0
    for i in range (0,9):
        for j in range (0,9):
            if fixed_sudoku[i,j] != 0:
                numberOfItterations += 1
    return numberOfItterations

def CalculateInitialSigma (sudoku, fixedSudoku, listOfBlocks):
    listOfDifferences = []
    tmpSudoku = sudoku
    for i in range(1,10):
        tmpSudoku = ProposedState(tmpSudoku, fixedSudoku, listOfBlocks)[0]
        listOfDifferences.append(CalculateNumberOfErrors(tmpSudoku))
    return (statistics.pstdev(listOfDifferences))


def solveSudoku (sudoku):
    f = open("demofile2.txt", "a")
    solutionFound = 0
    while (solutionFound == 0):
        decreaseFactor = 0.99
        stuckCount = 0
        fixedSudoku = np.copy(sudoku)
        PrintSudoku(sudoku)
        FixSudokuValues(fixedSudoku)
        listOfBlocks = CreateList3x3Blocks()
        tmpSudoku = RandomlyFill3x3Blocks(sudoku, listOfBlocks)
        sigma = CalculateInitialSigma(sudoku, fixedSudoku, listOfBlocks)
        score = CalculateNumberOfErrors(tmpSudoku)
        itterations = ChooseNumberOfItterations(fixedSudoku)
        if score <= 0:
            solutionFound = 1

        while solutionFound == 0:
            previousScore = score
            for i in range (0, itterations):
                newState = ChooseNewState(tmpSudoku, fixedSudoku, listOfBlocks, sigma)
                tmpSudoku = newState[0]
                scoreDiff = newState[1]
                score += scoreDiff
                print(score)
                f.write(str(score) + '\n')
                if score <= 0:
                    solutionFound = 1
                    break

            sigma *= decreaseFactor
            if score <= 0:
                solutionFound = 1
                break
            if score >= previousScore:
                stuckCount += 1
            else:
                stuckCount = 0
            if (stuckCount > 80):
                sigma += 2
            if(CalculateNumberOfErrors(tmpSudoku)==0):
                PrintSudoku(tmpSudoku)
                break
    f.close()
    return(tmpSudoku)

solution = solveSudoku(sudoku)
print(CalculateNumberOfErrors(solution))
PrintSudoku(solution)

By the way, there is great guy posted 10 different solving strategies. In addition, in previous blog, I also detailed the applying of Linear Programing (LP) to solve Sudoku, which doesn’t require fancy iterative algos but simple math optimization(derivative calculation).