According to wiki, “in mathematics, a Lie group (pronounced /liː/ LEE) is a group that is also a differentiable manifold. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract concept of a binary operation along with the additional properties it must have to be a group, for instance multiplication and the taking of inverses (division), or equivalently, the concept of addition and the taking of inverses (subtraction). Combining these two ideas, one obtains a continuous group where multiplying points and their inverses are continuous. If the multiplication and taking of inverses are smooth (differentiable) as well, one obtains a Lie group. As to the history of Lie groups (Hawkins, p. 1), Sophus Lie himself considered the winter of 1873–1874 as the birth date of his theory of continuous groups

Lie group, continuous group, contains infinite element and can be described with finite continuous parameters. The number of these parameters are called the dimension of Lie group.

Following a Chinese professor on Lie Group and it’s application on physics.

examples

Similarly Lorentz Transformation also required 10 dimensions, i.e. Galileo Group. Minkowski space Poincare transformation forms Poincare Group.

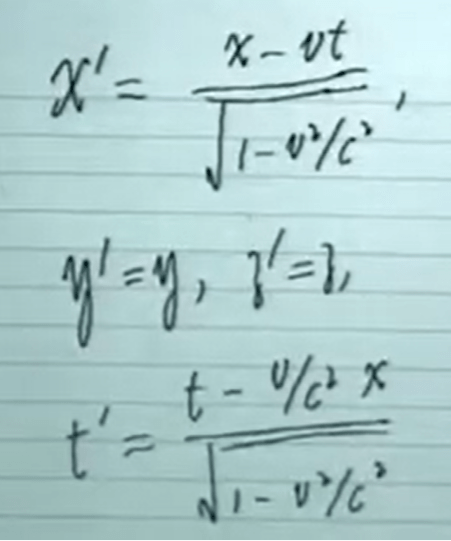
Strictly to have a Lie Group G, it is first has to be a group satisfying 4 conditions, it also has to be a differential manifold whose multiplication and reverse computation are smooth.

We can relate to partial derivative thinking about the transforming of Lie Group G, fixing/defining e as the element when no parameter/dimension changes.

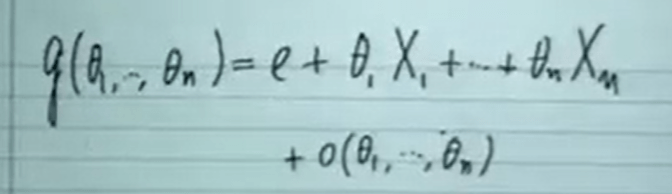
Commutator’s properties: enclosed, dual linear, substitutable, and the Jacobian identity:

交替性和反对称性可以互推， 但不是完全相同。