This part is about set definition and basics.

“Predicates” is one of the very basic/important concept in set theory. What is “predicate”? It’s an expression with undetermined variables that ascribes a property to objects filled in for the variables. It is used to form new sets for example below, for all element x in N, that fulfill the property that x is an even number, forms a set. Once fulfilled, the statement (or set?) becomes a logical statement/proposition. So my understanding is that the part to the right of vertical “x is an even number” is the predicate in this example.

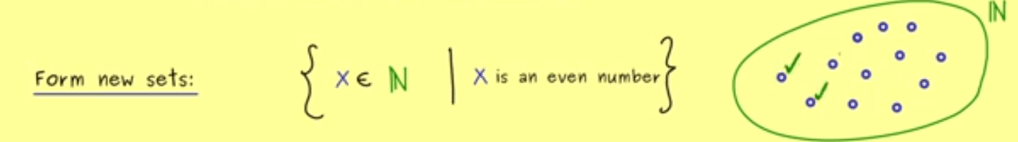
“Quantifiers” is the other very important/basic concept. The sign is universal one is “for any” and the other is “it exists”. so a statement x is a planet is not a proposition, but “for any x, x is a planet” is a proposition because every x is checked. note the collen here read as s.t. i.e. such that.

Grasping both “predicate” and “quantifier” leads to the understanding of concept of “equality“:

When we say two sets A and B are the same, written as A = B if for all x, such that “x in A if and only if x is in B”. “x in A if and only if x is in B” is the predicate, once quantifier “for all x” is added, then it is a logical statement or proposition.

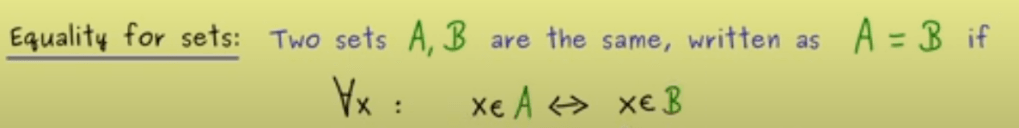
Based on above logical statement one can prove if

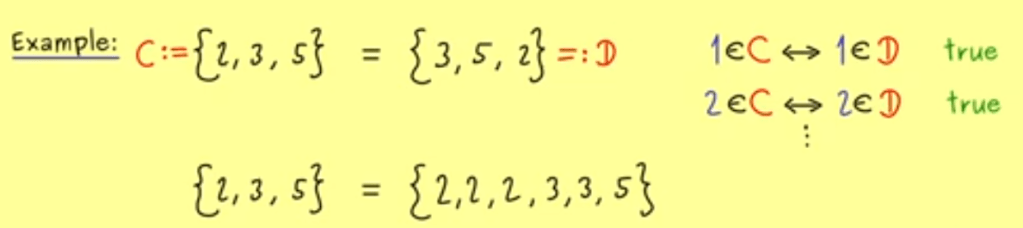
Following the same rigor, definition of “subsets” are:

There is the “big union” concept was not familiar before:

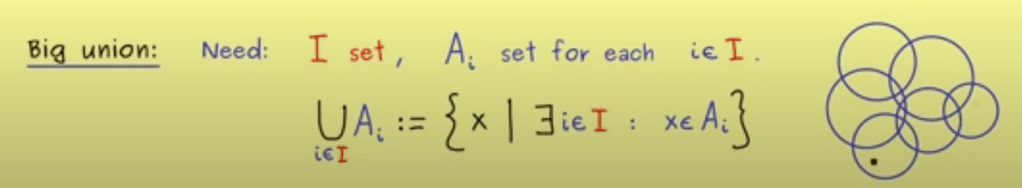
Here is an example to make it concrete:

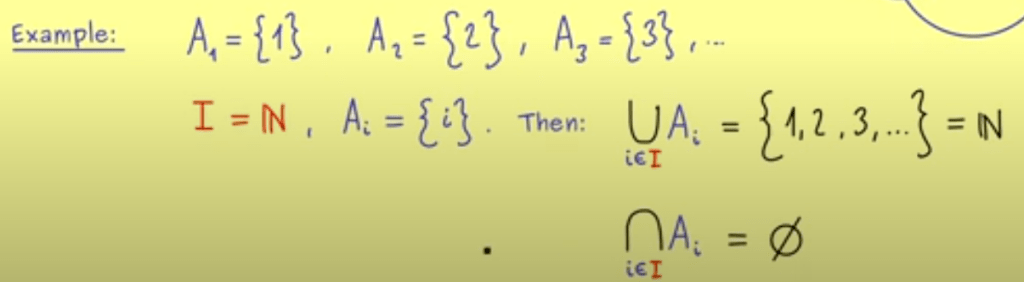
Leading to an important notion “Power Set“, Power set is a set for all subsets. Accurately, for a set A define:

one can see the relationship between “the number of element in set A” and “the number of element in power set of A”. |A| = 3 |P(A)| = 2^3 = 8.